3.2. Задача о ранце

Напомним линейную булеву задачу о ранце, постановка которой приведена в Главе 1. Задана емкость ранца B>0 и множество предметов N={1,…,N}, каждый из которых JÎN имеет “ценность” Cj И “вес” Aj ³ 0. Требуется выбрать подмножество предметов максимальной суммарной ценности, общий вес которых не превосходит емкости ранца B. Вводя переменные Xj=1, если предмет JÎN кладется в ранец и Xj=0 в противном случае, запишем математическую модель проблемы:

Z=	(3.2)
	(3.3)

Для L=0,1,...,b и векторов (x1,...,xK), K=1,...,n рассмотрим семейство задач (PK(L)):

Sk(L)=

Очевидно, оптимальное значение целевой функции исходной задачи (3.2)-(3.3) равно Z=SN(b). Заметим также, что

· если =0, то SK(L)=SK-1(L);

· если =1, то SK(L)=Ck+SK-1(L - Ak).

Отсюда следуют рекуррентные соотношения:

.

(3.4)

Имеем S1(L)=0 при 0£ L < a1 и S1(L)=Max{0,c1} ПриL ³ a1. Далее, используя (3.4), находим S2(L),...,SN(L) Для всех L=0,...,b.

На обратном ходе ДП строится оптимальное решение задачи (3.2)-(3.3). Во время прямого хода мы можем запоминать все условно-оптимальные решения Xk(L), K=1,…N, L=0,1,...,b: Xk(L)=0, если SK(L)=SK-1(L), И Xk(L)=1, в противном случае. Решение восстанавливается с последней компоненты. Положим K=N, L=B. Если Xk(L)=0, то ввиду SK(L)=SK-1(L), полагаем =0. Если Xk(L)=1, то SK(L)=сK+SK-1(L-Ak) и полагаем =1. Если K >1, то полагаем K=K-1, L=L-AnИ повторяем итерацию.

Как видно, оптимальное решение NP-трудной булевой задачи о ранце строится алгоритмом ДП с Псевдополиномиальной трудоемкостью O(nb).

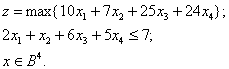Разберем

Пример 3.3. Решить задачу

Воспользуемся соотношениями (3.4) и заполним Табицу 3.1, в каждой клетке (L,SK(L)) Которой, наряду со значением SK(L), будем запоминать условно-оптимальные решения Xk(L) (после символа “/”).

В результате прямого хода найдено оптимальное значение целевой функции S4(7)=34 и последней компоненты вектора-решения X4(7)=1. Следовательно, =1. Полагаем K =3, L = L - A4 = 7 - 5 = 2. Строка L = 2 и столбец S2(2) Таб. 3.1 позволяют найти =0. Следовательно, полагаем K =2, L = L - A3 = 2 - 0 = 2. Из таблицы видно также, что =0, а =1.

В Таб. 3.1 затемнены клетки, позволившие восстановить оптимальное решение задачи.

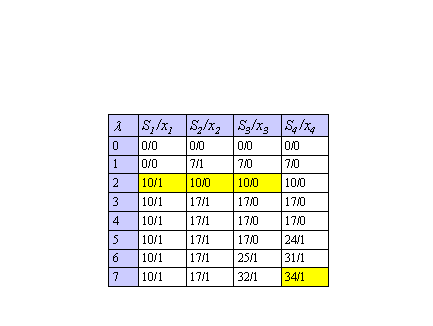Таб. 3.1.

Пусть теперь переменные задачи о ранце принимают целочисленные неотрицательные значения. Задача перепишется в виде

Z=	(3.5)
	(3.6)

Погрузим задачу (3.5)-(3.6) в семейство {(P(A)), A=0,1,…,A}, где задача (P(A)):

S(A)=

Теорема 3.1. Для задачи (3.5)-(3.6) справедливы рекуррентные соотношения:

S(A) = {S(A - ak) + ck}, 0£ A £ A.

(3.7)

(Максимум по пустому множеству полагаем равным нулю.)

Доказательство. Пусть X*(A) – оптимальный вектор. Тогда S(A) = (C, X*(A)). Если S(A)>0, то существует такой номером K, что X(A)>0 и (C, X*(A)) = (C, X*(A) - Ek) + Ck, где Ek – K-й орт. Значит

S(A) £ S(A - Ak) + Ck £ {S(A - Ak) + Ck}.

С другой стороны

{S(A - ak) + ck}= S(A - ai) + ci = (c, x*(A - ai)) + ci =

(C, X*(A - Ai) + Ei) £ (C, X*(A)) = S(A). ¨

Соотношения (3.7) позволяют найти оптимальное значение функционала (3.5). Оптимальное решение находится по следующей процедуре.

Обратный ход. Положим X*=0, A*=А. Затем последовательно решаем уравнение:

S(A*) = S(A* - ak) + ck, ak £ A*

(3.8)

Относительно индекса K.

Если I – решение уравнения (3.8), то полагаем X= X+ 1; A*= A* - Ai и повторяем итерацию. Если уравнение (3.8) не имеет решения, тогда вектор X* оптимален.

Отношения (3.7) в случае целочисленных весов Ak, позволяют решить задачу (3.5)-(3.6) с псевдополиномиальной трудоемкостью - O(An) И памятью - O(A+N).

С задачей (3.5)-(3.6) тесно связана, так называемая, обратная задача:

	(3.9)
	(3.10)

Как и ранее, погрузим последнюю задачу в семейство {((B)), B=0,1,…,B}, где задача ((B)):

Q(B)=

Пусть X0(B) – оптимальное решение задачи ((B)).

Лемма 3.2. Функция Q(B) является неубывающей.

Доказательство. Пусть B2>B1. Очевидно, X0(B2) - допустимое решение задачи ((B1)). Следовательно, Q(B2)=(A, X0(B2))³ Q(B1).¨

Для обратной задачи справедливы рекуррентные соотношения:

Q(0) = 0; Q(B) = {Q(Max{0, B - Ck}) + Ak}, 0 £ B £ B,

Благодаря которым оптимальное решение строится с трудоемкостью – O(NB) и памятью – O(B+N).

Теорема 3.2. (связь прямой и обратной задач о ранце). Пусть = Max{B| Q(B) £ A, B ³ 0}. Тогда S(A)= и оптимальное решение X0() обратной задачи (()) является оптимальным и для прямой задачи (P(A)).

Доказательство. Обозначим S*= S(A). Так как X*(A) – допустимый вектор для обеих задач ((S*)) и (P(A)), то Q(S*) (A, X*(A)) £ A. Из неравенства Q(S*) £ A и определения следует, что ³ S*. С другой стороны, так как оптимальное решение X0() обратной задачи (()) Является допустимым для прямой задачи (P(A)) (так как (A, X0()) = Q() £ A), то (C, X0()) £ (C, X*(A)) = S* . Значит, = S* = S(A) и (C, X0()) = S(A).¨

Следствие 3.1. В случае целочисленных Ck и произвольных Ak для решения прямой задачи о ранце можно использовать алгоритм ДП, имеющий трудоемкость O(NS*) и память O(S*+N), где S*=S(A)£ A Ck.

Доказательство. Из Леммы 3.1 и Теоремы 3.2 следует, что

S* = min{B| A < Q(B+1), B = 0,1,…}.

Значит, можно применить следующий алгоритм.

- Во время работы прямого хода вычислить Q(B), полагая последовательно B = 0,1,…, пока для некоторого не получим неравенство А< Q(+1). Это и есть оптимальное значение целевой функции S* прямой задачи (P(A)).

- На обратном шаге, зная значения Q(B), B=0,1,…,S*, найдем оптимальное решение X0(S*) обратной задачи ((S*)), которое является также искомым решением X*(A) прямой задачи (P(A)).¨

Сформулируем аналогичные утверждения, позволяющие перейти от обратной задаче к прямой.

Теорема 3.3. Пусть = Min{A| S(A) ³ B, A ³ 0}. Тогда Q(В) = и оптимальное решение X*() Прямой задачи (P()) является также оптимальным решением X0(В) обратной задачи ((В)).

Следствие 3.2. В случае целых Ak И произвольных Ck обратная задача ((В)) Может быть решена алгоритмом ДП с трудоемкостью O(N) и памятью O(+ N), где =Q(B) £ B Ak.

Переход от прямой задаче к обратной и наоборот оправдан не только в случае нецелочисленности одной группы параметров и целочисленности другой. Иногда этот переход позволяет уменьшить трудоемкость реализации алгоритма ДП.

Задача о ранце в общем случае нелинейна. Функционал может быть задан произвольными сепарабельными функциями. Запишем общую формулировку:

S*=S(A)=	(3.11)
,	(3.12)

Где Fj Зависят только от Xj (свойство сепарабельности).

Как и прежде, наряду с задачей (3.11)-(3.12) рассмотрим семейство задач с количеством предметов K=1,…,N и емкостью ранца A=0,…,A. Обозначим через Sk(A) оптимальное значение функционала соответствующей задачи. Тогда для (3.11)-(3.12) справедливы соотношения:

S1(A) = F1(X1), 0£ A £ A;

Sk(A) = { Sk-1(A - Akxk) + Fk(Xk)}, K=2,…,N, 0£ A £ A.

Приведенные рекуррентные соотношения справедливы для любых Ak и Fk, но для конечности реализации алгоритма необходима конечность значений аргументов функций Sk(A). Для этого достаточно потребовать целочисленность Ak. Тогда достаточно перебрать конечное множество значений A=0,…,A.

< Предыдущая		Следующая >