§3.2. Признаки равномерной сходимости функциональных последовательностей и рядов

Теорема 1 (Критерий Коши равномерной сходимости функциональной последовательности):

Для того чтобы функциональная последовательность Сходилась равномерно на множестве Х к некоторой функции , необходимо и достаточно, чтобы "e>0 – натурального, , выполнялось следующее условие: .

Док-во: 1. Необходимость. Пусть последовательность равномерно сходится к функции на множестве Х, тогда выполняется , т. к. P – натуральное, то, очевидно, что и , используя свойства модуля, окончательно получаем – натурального, , ч. т.д.

2. Достаточность. Пусть – натурального

Условие (1) означает, что последовательность является фундаментальной числовой последовательностью и, следовательно, сходится к некоторому числу, зависящему от выбора Х. Таким образом, функциональная последовательность сходится на множестве Х при , а значит и последовательность также сходится к при , где p – натуральное. Переходя к пределу при в неравенстве (1): , а это и означает, что , ч. т.д.

Теорема 1’ (Критерий Коши равномерной сходимости функционального ряда):

Для того, чтобы функциональный ряд равномерно сходился к своей сумме необходимо и достаточно, чтобы – натурального, , выполнялось .

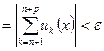Док-во: Аналогично доказательству Теоремы 1.

< Предыдущая		Следующая >