§1. Поверхностные интегралы. Площадь поверхности

Площадь поверхности, заданной явным образом.

Z = F(X,Y), где функция F(X,Y) определена в замкнутой ограниченной области G, при этом функция F(X,Y) имеет в области G непрерывные частные производные второго порядка. Произведем разбиение поверхности P кусочно-гладкими линиями. Фрагменты разбиения на поверхности обозначим, как Pi, Проведем через точку Mi касательную плоскость к поверхности Pi. При этом ту часть плоскости, которая проецируется на Gi обозначим Si.И такую процедуру проведем для всех фрагментов Pi.Тем самым рассматриваемая поверхность окажется покрытой фрагментами касательных плоскостей. Полученная конструкция (скорее всего) не является многогранником в привычном смысле. Введем сумму

Пусть Di максимальный диаметр Pi, а D – максимальный диаметр по всем фрагментам разбиения.

Определение: Число S называется пределом при сумм вида 1, если для любого существует такое, что для любого разбиения Pi , такого, что :

Если существует такой предел, то поверхность Р называется квадрируемой, а число S – площадью этой поверхности.

Теорема 1: Пусть функция определена в замкнутой ограниченной области G, в которой она имеет непрерывные частные производные первого порядка, тогда фигура задаваемая данной функцией является квадрируемой, и ее площадь вычисляется по следующей формуле:

Док-во: Рассмотрим некоторый фрагмент разбиения Pi, на котором произвольный образом выберем точку Mi. Замкнем уравнение касательной к плоскости к функции

Вектор нормали в точке Mi . Пусть – угол между нормалью и осью Oz. Вычислим

Пусть – площадь области в плоскости OXy, на которую проецируется поверхность Pi, тогда справедливо . Таким образом, получаем, что площадь Si будет равна

Рассмотрим сумму

Правая часть выражения (3) при представляет собой интегральную сумму (для случая двойного интеграла) для функции , заданной на области G. В условиях указанной теоремы предел указанной суммы существует, а следовательно существует следующий предел:

, ч. т.д.

Пример: Вычислить площадь параболоида вращения, ограниченного .

Перейдем к полярным координатам . Следовательно, получаем:

Замечание: Поверхности также могут задаваться и неявным образом. Но основной способ задания поверхностей (в смысле общности) – это параметрический способ задания поверхностей.

Площадь поверхности, заданной параметрически.

Параметрическое задание поверхности определяется следующими формулами:

Фиксировав параметр V и изменяя параметр U, радиус-вектор опишет на нашей поверхности некоторую линию. Таким образом, фиксируя разные значения, соответствующие параметрам U и V, получим криволинейную систему координат на поверхности. (Рассматриваемая поверхность является двумерной) Вычислим производные вектора R:

;

;

Плоскость, проходящая через данную точку M и содержащая вектора Ru и Rv, является касательной к данной поверхности. Поэтому вектор нормали

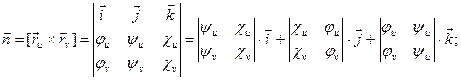
Суммируя по всем элементарным сегментам разбиения, получаем следующую формулу для вычисления площади поверхности D.

Рассмотрим модуль векторного произведения:

Откуда

Замечание (О вычислении длины на криволинейной поверхности):

Рассмотрим поверхность, а на ней достаточно близкие точки. Поставим перед собой вопрос о вычислении кратчайшей линии, которая соединяет две точки и . В том случае, когда точки M и N бесконечно близки, расстояние Dl вычисляется как длина вектора Dl:

На самом деле в дифференциальной геометрии квадрат элемента длины определяется следующей формулой (через E, F и G):

называется первой квадратичной формой поверхности, или метрикой поверхности. По первой квадратичной форме формулы (3) на поверхности измеряются линии, углы между линиями. Первая квадратичная форма определяет внутреннюю геометрию поверхности, которая определяет форму поверхности в пространстве. Чтобы поверхность была однозначно заданной необходимо задать и первую и вторую квадратичные формы поверхности.

Пример: Вычислим площадь обычной сферы. Введем сферические координаты.

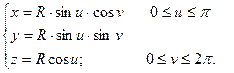
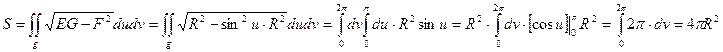
Следующая >