§1.23. Формула Тейлора

Теорема

Пусть функция - (n+1) раз дифференцируема в точке M тогда приращение функции в окрестности данной точки представимо в виде

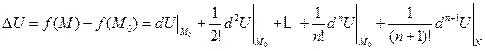
Точка N в последнем остаточном члене в правой части также лежит в рассматриваемой окрестности и, вообще говоря, зависим от т. М

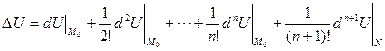(1)

В окрестности точки:

Где 0<q<1.

Вычисляя дифференциал, получаем:

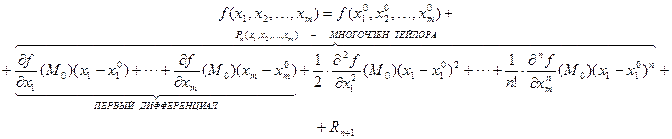
Многочлен Тейлора характеризуется тем свойством, что его значения в точке М0 и его производных в точке М0 совпадает со значением функции F(M0) И производных функции F(M0) В точке М0.

< Предыдущая		Следующая >