§1.16. Дифференцируемость функции

Опр.: Функция U=F(M) называется дифференцируемой в данной точке, если её приращение в этой точке представимо в виде:

, (*)

Где - константы,

А при .

Функции - бесконечно малые функции аргумента в нуле.

Рассмотрим функцию ,

,

.

Таким образом, перепишем приращение в виде:

.

, I=1,…,m,

.

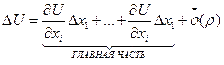Опр.: Дифференциалом функции U=F(M) называется главная линейная часть приращения функции.

Дифференциалом независимой переменной назовём ,

Тогда дифференциал функции вычисляется по следующим правилу:

.

Дифференциал функции M переменных представляет собой функцию 2M переменных:

и - независимые переменные.

Утверждение:

Если функция U=F(M) дифференцируема в данной точке, то функция непрерывна в данной точке. Обратное неверно.

Согласно (*) рассмотрим предел приращения:

=> U – непрерывна, что и составляет разностную форму непрерывности функции.

Пример:

- непрерывна, но не является дифференцируемой.

 

< Предыдущая		Следующая >