09. Распределение Пуассона

(Симеон Дени Пуассон (1781 – 1840) – французский математик)

Пусть производится П независимых испытаний, в которых появление события А имеет вероятность Р. Если число испытаний П достаточно велико, а вероятность появления события А в каждом испытании мало (P£0,1), то для нахождения вероятности появления события А K раз находится следующим образом.

Сделаем важное допущение – произведение Пр сохраняет постоянное значение:

Практически это допущение означает, что среднее число появления события в различных сериях испытаний (при разном П) остается неизменным.

По формуле Бернулли получаем:

Найдем предел этой вероятности при П®¥.

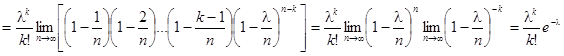
Получаем формулу Распределения Пуассона:

Если известны числа l и K, то значения вероятности можно найти по соответствующим таблицам распределения Пуассона.

< Предыдущая		Следующая >