18. Свойства плотности распределения

1) Плотность распределения – неотрицательная функция.

2) Несобственный интеграл от плотности распределения в пределах от - ¥ до ¥ равен единице.

Пример. Случайная величина подчинена закону распределения с плотностью:

Требуется найти коэффициент А, построить график функции плотности распределения, определить вероятность того, что случайная величина попадет в интервал от 0 до .

Построим график плотности распределения:

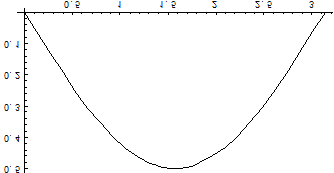
Для нахождения коэффициента А воспользуемся свойством .

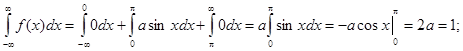
Находим вероятность попадания случайной величины в заданный интервал.

Пример. Задана непрерывная случайная величина Х своей функцией распределения F(X).

Требуется определить коэффициент А, найти функцию распределения, построить графики функции распределения и плотности распределения, определить вероятность того, что случайная величина Х попадет в интервал .

Найдем коэффициент А.

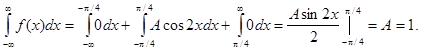
Найдем функцию распределения:

1) На участке :

2) На участке

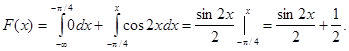
3) На участке

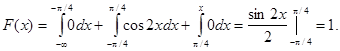
Итого: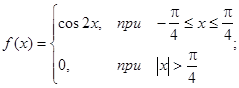

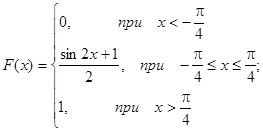
Построим график плотности распределения:

F(X)

Построим график функции распределения:

F(x)

Найдем вероятность попадания случайной величины в интервал .

Ту же самую вероятность можно искать и другим способом:

< Предыдущая		Следующая >