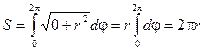60. Вычисление длины дуги кривой

y y = f(x)

DSi Dyi

Dxi

a b x

Длина ломаной линии, которая соответствует дуге, может быть найдена как .

Тогда длина дуги равна .

Из геометрических соображений:

В то же время

Тогда можно показать (см. Интегрируемая функция.), что

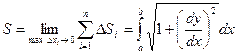
Т. е.

Если уравнение кривой задано параметрически, то с учетом правил вычисления производной параметрически заданной функции (см. Производная ФУнции, заданной параметрически.), получаем

,

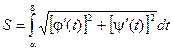Где х = j(t) и у = y(t).

Если задана Пространственная кривая, и х = j(t), у = y(t) и z = Z(t), то

Если кривая задана в Полярных координатах, то

, r = f(j).

Пример: Найти длину окружности, заданной уравнением x2 + y2 = r2.

1 способ. Выразим из уравнения переменную у.

Найдем производную

Тогда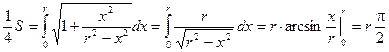

Тогда S = 2pr. Получили общеизвестную формулу длины окружности.

2 способ. Если представить заданное уравнение в полярной системе координат, то получим: r2cos2j + r2sin2j = r2, т. е. функция r = f(j) = r, тогда

< Предыдущая		Следующая >