49. Вычисление определенного интеграла

Пусть в интеграле нижний предел а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение интеграла.

Обозначим = Ф(х). Найдем производную функции Ф(х) по переменному верхнему пределу х.

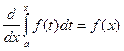
Аналогичную теорему можно доказать для случая переменного нижнего предела.

Теорема: Для всякой функции f(x), непрерывной на отрезке [a, b], существует на этом отрезке первообразная, а значит, существует неопределенный интеграл.

Теорема: (Теорема Ньютона – Лейбница)

Если функция F(x) – какая - либо первообразная от непрерывной функции f(x), то

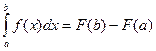
Это выражение известно под названием формулы Ньютона – Лейбница.

Доказательство: Пусть F(x) – первообразная функции f(x). Тогда в соответствии с приведенной выше теоремой, функция - первообразная функция от f(x). Но т. к. функция может иметь бесконечно много первообразных, которые будут отличаться друг от друга только на какое – то постоянное число С, то

При соответствующем выборе С это равенство справедливо для любого х, т. е. при х = а:

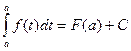
Тогда .

А при х = b: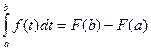

Заменив переменную t на переменную х, получаем формулу Ньютона – Лейбница:

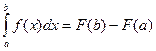
Теорема доказана.

Иногда применяют обозначение F(b) – F(a) = F(x).

Формула Ньютона – Лейбница представляет собой общий подход к нахождению определенных интегралов.

Что касается приемов вычисления определенных интегралов, то они практически ничем не отличаются от всех тех приемов и методов, которые были рассмотрены выше при нахождении неопределенных интегралов.

Точно так же применяются методы подстановки (замены переменной), метод интегрирования по частям, те же приемы нахождения первообразных для тригонометрических, иррациональных и трансцендентных функций. Особенностью является только то, что при применении этих приемов надо распространять преобразование не только на подинтегральную функцию, но и на пределы интегрирования. Заменяя переменную интегрирования, не забыть изменить соответственно пределы интегрирования.

< Предыдущая		Следующая >