45. Однофакторный дисперсионный анализ
Большое количество практических задач приводится к задачам однофакторного дисперсионного анализа.
Типичным примером является работа технологической линии в составе которой имеется несколько параллельных рабочих агрегатов.
На выходе имеют место какие-то детали. Эти детали по какому-то параметру можем контролировать.
Ясно, что среднее значения контролируемых параметров после каждого станка будут несколько отличаться.
Вопрос: Обусловлены ли эти отличия действием случайных факторов или имеет место влияние конкретного станка агрегата.
В данном случае фактор только один – станок.
Совокупность размеров деталей подчиняется нормальному закону распределения, и все эти совокупности имеют равные дисперсии.
Имеется m станков, т. о. имеется m совокупностей. Из этих совокупностей мы проводим выборки объёмом n. Так, что значение параметров i-той совокупности i: ![]() .
.
Все выборки можно записать в виде таблицы, которая называется Матрицей наблюдения.
I \ j |
1 |
2 |
. |
J |
. |
N |
Ср. выборочное |
|
1 |
X11 |
X12 |
. |
X1j |
. |
X1n |
|
|
2 |
X21 |
X22 |
. |
X2j |
. |
X2n |
|
|
. |
. |
. |
. |
. |
. |
. |
. |
|
I |
Xi1 |
Xi2 |
. |
Xij |
. |
Xin |
|
|
. |
. |
. |
. |
. |
. |
. |
. |
|
M |
Xm1 |
Xm2 |
. |
Xmj |
. |
Xmn |
|
Выдвигаем гипотезу Н0 заключающуюся в равенстве средних выборочных.
![]()
Гипотеза Н0 проверяется сравнением внутригрупповых и межгрупповых дисперсий по F критерию Фишера.
Если расхождение незначительно, то принимается гипотеза Н0, в противном случае гипотеза Н0 отвергается.
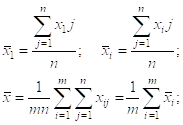
Далее находят сумму квадратов отклонений от общего среднего:
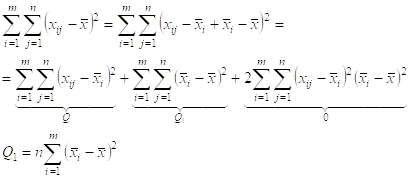
Ноль потому, что стоит сумма от ![]() - сумма отклонений переменных одной совокупности от средней арифметической той же совокупности.
- сумма отклонений переменных одной совокупности от средней арифметической той же совокупности.
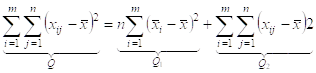
Слагаемое Q1 является суммой квадратов разностей между средними отдельных совокупностей и общей средней всех совокупностей. Эта сумма называется суммой квадратов отклонений между группами. Она характеризует систематическое отклонение между совокупностями наблюдений.
Величину Q1 – рассеяние по фактору.
Слагаемое Q2 – представляет собой сумма квадратов разностей между отдельными и средней соответствующей совокупности. Эта сумма называется суммой квадратов отклонений внутри группы.
Она характеризует остаточное рассеяние случайных погрешностей совокупностей.
Величина Q называется общей или полной суммой квадратов отклонений отдельных отклонений от общей средней.
Получим оценки дисперсий:![]()
- дисперсия обусловленная влиянием фактора;
![]() - остаточная дисперсия – влиянием случайных и других неучтённых факторов.
- остаточная дисперсия – влиянием случайных и других неучтённых факторов.
![]() - полная дисперсия.
- полная дисперсия.
Далее формируем оценку различия между оценками ![]()
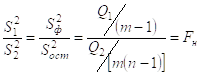 подчиняется распределению F2 Фишера.
подчиняется распределению F2 Фишера.
Выбираем уровень значимости α, или доверительной вероятности 1– α = Р и по таблице F-распределения с числом степеней свободы: к1 = m–1; к2 = m(n–1) находим критическое значение ![]() Фишера.
Фишера.
![]()
Сравнивая между собой Fн и Fкр,α мы делаем вывод насколько сильно влияние интересующего нас фактора на исследуемую случайную величину.
В этом и состоит идея дисперсионного анализа.
Однофакторный дисперсионный анализ обычно представляют в виде таблицы.
|
Компоненты дисперсии |
Оценки дисперсии |
Число степеней свободы | |
|
Основной фактор |
Межгрупповая дисперсия |
|
M - 1 |
|
Случайные, неучтенные факторы |
Внутригрупповая дисперсия |
|
M(n - 1) |
|
Общая дисперсия |
|
Mn - 1 |
| < Предыдущая | Следующая > |
|---|