30. Метод моментов (Метод Пирсона)

Метод обладает следующими достоинствами:

1. Оценки получаемые этим методом всегда являются состоятельными.

2. Метод моментов мало зависит от закона распределения случайной величины.

3. Сложность вычисления незначительна.

Известна случайная величина Х, которая характеризуется f(x, θ1, θ2…θq), аналитический вид этой функции известен.

По выборке объёмом n х1,х2,х3,…хn – значения случайной величины в выборке вычисляем эмпирические начальные моменты случайной величины:

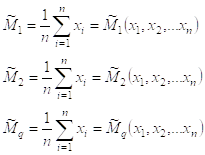
Находим теоретические моменты:

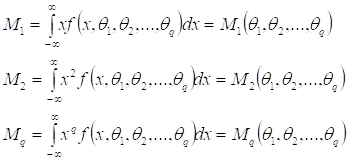
Основная идея метода моментов заключается в приравнивании значения эмпирических значений моментов теоретическим.

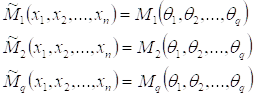
Решим систему q-уравнений с q-неизвестными:

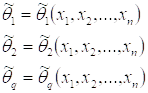состоятельные оценки.

Состоятельность этих оценок основана на том, что эмпирические моменты при достаточно большом n (n→∞) стремится к теоретическим. Выполняется закон больших чисел.

< Предыдущая		Следующая >