23. Центральная предельная теорема Ляпунова

Предмет внимания этой теоремы – распределение суммы большого числа СВ.

X=(x1+x2+…+xn)/n

Распределение суммы n независимых СВ в независимости от их законов распределения асимптотически сходятся к нормальному закону при неограниченном числе слагаемых и ограниченных двух первых моментах (МО и D).

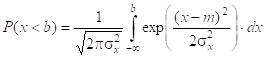
Если si2=s2, то sх2=s2/n, .

D(x)=sх2=(s12+s22+…sn2)/n2

ЦПТ универсальны и справедливы как для НСВ, так и для ДСВ.

P(a<X<b)=Ф(t2)-Ф(t1).

T2=(b-mx)/sx t2=(a-mx)/sx

Sn=(X1+X2+…+Xn)/n

P(|Sn-m|<zs)=2Ф(z)

M(xk)=m D(xk)=s2

< Предыдущая		Следующая >