17. Двумерные функции распределения

X, Y F(x, y)=P(X<x, Y<Y)

Функция F(X,Y) обладает свойствами, аналогичными свойствам одномерной функции:

– не убывающая 1. x2³x1 Þ F(x2,y)³F(x1,y)

– не отрицательная y2³y1 Þ F(x, y2)³F(x, y1)

0£F(x, y)£ 1 2. F(¥,¥)= 1 F(-¥,-¥)=0

3. Fx(x)=P(X<x+=P(X<x, Y<¥)=F(x,¥)

Fy(y)=P(Y<y)=P(X<¥,Y<y)=F(¥,y)

F(X,Y) – Функция плотности вероятности совместного распределения величин X и Y.

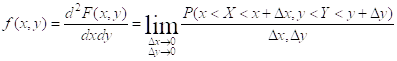
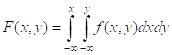
1. f(x, y)³0

2. 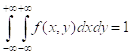– условие нормировки

3. По известным двумерным находятся соответствующие одномерные

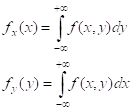
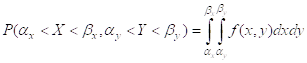
В случае статистической независимости СВ Х и У

F(x, y)=Fx(x)×Fy(y)

F(x, y)=fx(x)×fy(y)

F(x, y)=Fx(x)×Fy(y/x)=Fx(x/y) – для условных

F(x, y)=fx(x) ×f(y/x)=fy(y) ×f(x/y)

< Предыдущая		Следующая >