36. Уравнение плоскости, проходящей через три заданные точки
Точка M(X,Y,Z) лежит на плоскости. Значит три вектора компланарны:

![]()
![]()
![]()
Уравнение плоскости получится из условия компланарности трех векторов, а именно: смешанное произведение трех векторов равно нулю:
![]()
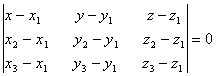
Нормированное уравнение плоскости. Отклонение точки от плоскости.
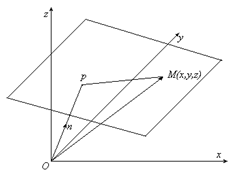 Поставим цель выразить уравнение плоскости через длину отрезка
Поставим цель выразить уравнение плоскости через длину отрезка ![]() = р и направляющие косинусы единичного вектора
= р и направляющие косинусы единичного вектора ![]() . Очевидно, точка М лежит на нужной нам плоскости тогда и только тогда, когда
. Очевидно, точка М лежит на нужной нам плоскости тогда и только тогда, когда ![]() или
или ![]() , но:
, но: ![]() и тогда уравнение искомой плоскости, очевидно будет:
и тогда уравнение искомой плоскости, очевидно будет: ![]() .
.
Так же как и в случае уравнения линии, назовем отклонением точки М от плоскости ее расстояние до плоскости со знаком (-), если точка М и начало координат лежат в одной стороне от плоскости и со знаком (+), если по разные стороны. Тогда можно доказать, что для нахождения отклонения d точки М от плоскости необходимо в левую часть нормированного условия плоскости подставить на место X, Y и Z координаты X0 Y0 Z0 точки М0.
Как привести уравнение плоскости к нормированному виду. Поскольку
![]()
Одна и та же плоскость, то, очевидно, найдется такое число t, что:
T A = cos A ; t B = cos B; t C = cos G ; t D = - p ;
Из первых трех уравнений имеем: ![]() , отсюда расстояние плоскости от начала координат
, отсюда расстояние плоскости от начала координат ![]() . Из четвертого равенства, поскольку p всегда положительно, следует знак у t брать противоположный D.
. Из четвертого равенства, поскольку p всегда положительно, следует знак у t брать противоположный D.
| < Предыдущая | Следующая > |
|---|