04. Директрисы эллипса и гиперболы

Определение. Прямые х=(А/ε), где ε — эксцентриситет эллипса (гиперболы) называются директрисами эллипса (гиперболы).

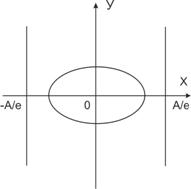
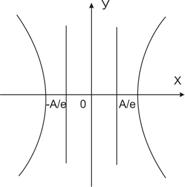
Теорема. Отношение расстояния от любой точки эллипса (гиперболы) до фокуса к расстоянию до соответствующей директрисы есть величина постоянная, равная эксцентриситету эллипса (гиперболы).

Доказательство, например для эллипса, следует из того, что

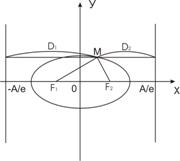MF1=а+εх, МF2=а—εх.

Заметим, что, так как все точки параболы равноудалены от директрисы и фокуса, то отношение этих расстояний равно 1. Поэтому можно говорить об эксцентриситете параболы и считать его равным 1. Как уже отмечалось, эксцентриситет окружности равен нулю.

 

 

 

 

 

< Предыдущая		Следующая >