02. Эллипс
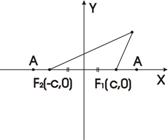 Определение. Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек F1 и F2 этой плоскости, называемых фокусами эллипса, есть величина постоянная, равная 2А (А>0), большая, чем расстояние между фокусами.
Определение. Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек F1 и F2 этой плоскости, называемых фокусами эллипса, есть величина постоянная, равная 2А (А>0), большая, чем расстояние между фокусами.
Для составления уравнение эллипса выберем прямоугольную декартову систему координат так, чтобы ось ОХ
Проходила через фокусы F1 и F2, а начало координат — точка О находилась в середине отрезка F1F2.
Обозначим F1F2 = 2с. Тогда F1(-с,0), F2(c,0). Пусть М(х, у) – произвольная точка эллипса. Тогда MF1+ MF2= 2А, а>с.
Так как ![]() , и уравнение принимает вид:
, и уравнение принимает вид:
 . (2)
. (2)
Пусть координаты точки М1(х1,у1)удовлетворяют уравнению (2).
Обозначим r1 = F1M1, r2 = F2M2 — Фокальные радиусы точек М1 М2. Тогда 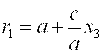 ,
, 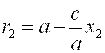 , значит, r1+r2=2A.
, значит, r1+r2=2A.
Теперь по свойствам уравнения (2) исследуем геометрические свойства эллипса.
1. Оси ОХ и ОУ являются осями симметрии эллипса. Следовательно, эллипс достаточно исследовать только в первой координатной четверти.
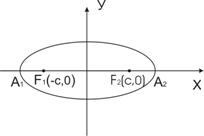
2. Эллипс пересекает координатные оси в точках А1(-А,0), А2(А,0), В1(0,B), В2(0,-B), называемых Вершинами эллипса.
3. Эллипс расположен в прямоугольнике, ограниченном прямыми х=![]() А, у =
А, у =![]() B.
B.
4. Из уравнений следует, что при возрастании х от 0 до А в первой координатной четверти, У убывает от B до 0.
По полученным свойствам строим эллипс Отрезок А1А2 и его длина 2А называются Большой осью эллипса, а отрезок B1B2 и его длина 2B называются Малой осью эллипса. Отрезок ОА1 с длиной А и отрезок ОВ1 с длиной B называются соответственно Большой и малой полуосями эллипса. Длина отрезка F1F2=2С Называется Фокусным расстоянием, начало координат — Центр эллипса.
 Если А=B, то получаем каноническое уравнение окружности
Если А=B, то получаем каноническое уравнение окружности
![]()
Уравнения х = ACost, у = BSint -
Параметрические уравнения эллипса.
Определение. Эксцентриситетом эллипса называется число

Так как с<А, то 0<C<1. Заметим, что у окружности оба фокуса
Совпадают, поэтому С = 0 и ε = 0.
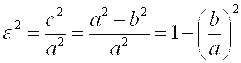 .
.
Следовательно, эксцентриситет характеризует форму эллипса.
Используя понятия эксцентриситета, можно выразить фокальные радиусы произвольной точки M(x, у) эллипса:
r1=А+εх, r2=А—εх
| < Предыдущая | Следующая > |
|---|