2.10. Дисперсионный анализ

В предыдущем параграфе мы рассмотрели схему проверки гипотезы о несущественности (незначимости) различия выборочных средних двух нормально распределенных случайных величин. Теперь рассмотрим обобщение этой задачи: требуется проверить гипотезу Н0 о несущественности (незначимости) различия выборочных средних M нормально распределенных случайных величин (M>2) при альтернативной гипотезе Н1 о том, что хотя бы некоторые из указанных выборочных средних различаются существенно (значимо).

Можно, конечно, опираясь на методику предыдущего параграфа, сравнить указанные выборочные средние попарно. Но для не слишком малых значений M это выливается в трудоемкую и громоздкую проблему. Гораздо эффективнее решается эта проблема с помощью так называемого Дисперсионного анализа, при котором сравниваются между собой не выборочные средние, а некие обобщенные дисперсии, о которых речь пойдет ниже.

На практике дисперсионный анализ применяют, когда хотят выяснить, оказывает или не оказывает влияние на нормально распределенную случайную величину Х некоторый Качественный фактор А, который имеет M различных качественных реализаций (уровней). Например, если Х – урожайность некоторой сельскохозяйственной культуры, то качественным фактором А, чье влияние на Х может исследоваться, может быть вид (марка) удобрения; или режим ухода за растениями (прополки, полива); или технология уборки, и т. д. А если Х – прибыль предприятия, то качественным фактором А, влияющим (или не влияющим) на прибыль Х, может быть технология производства; качество сырья; структура управления производством; система материального или морального стимулирования работников, и т. д.

Если исследуется влияние на величину Х лишь одного качественного фактора А, то говорят об однофакторном дисперсионном анализе. А если сразу нескольких – то о многофакторном.

С помощью дисперсионного анализа исследуется значимость влияния на наблюдаемую величину Х каждого из факторов, сравнивается их влияние между собой, устанавливается факт их взаимодействия, и т. д. Первоначально дисперсионный анализ был предложен Р. Фишером (1925 г.) для обработки результатов агрономических опытов. В дальнейшем этот метод стал использоваться всюду, где требуется математическая обработка результатов экспериментов.

Примечание. Если факторы, чье влияние на величину Х Исследуется, являются Количественными (уровни Каждого из таких факторов А – числа), то дисперсионный анализ можно применять и в этом случае. Но гораздо более емкие и глубокие выводы о характере влияния таких факторов на величину Х мы сделаем, если вместо дисперсионного анализа применим корреляционно-регрессионный анализ, которому будет посвящен следующий параграф.

Главная идея дисперсионного анализа, как однофакторного, так и многофакторного, заключается в расчленении общего объема вариации (колеблемости) значений случайной величины Х по источникам ее образования. В частности, при однофакторном дисперсионном анализе используется разложение

WОбщ=WA+WОст (4.1)

Где WОбщ – общий объем вариации изучаемой случайной величины Х; WА – объем вариации, обусловленный действием на величину Х фактора А; WОст остаточный объем вариации, вызванный действием всех остальных неучтенных и считающихся случайными факторов (помех). Последующее сравнение рассчитанных на одну степень свободы объемов вариации WA и WОст , то есть сравнение соответствующих этим объемам дисперсий и позволяет оценить существенность (значимость) влияния на изучаемую величину Х данного фактора А.

При двухфакторном дисперсионном анализе выясняется не только значимость каждого из факторов А и В в отдельности, но и значимость их взаимодействия АВ. Для это общая вариация представляется в виде

WОбщ=WА+В+WОст=WA+WB+WAB+WОст , (4.2)

А затем анализируются соотношения между величинами WA, WB, WAB и WОст (точнее, между дисперсиями ).

Мы ограничимся рассмотрением лишь однофакторного дисперсионного анализа, ибо многофакторный анализ много сложнее и осуществляется обычно не вручную, а с помощью стандартных программ на ЭВМ.

Итак, пусть Х – некоторая изучаемая случайная величина, и исследуется воздействие на нее некоторого фактора А, имеющего M различных фиксированных уровней (A1; A2;…; Am) (качественных или количественных). В частности, если Х – урожайность культуры, а А – удобрение, то качественными уровнями этого удобрения могут быть различные виды этого удобрения, а количественными уровнями – дозы вносимого удобрения. И т. д.

Будем считать, что проведено N измерений величины Х при каждом из M уровней фактора А, так что таблица опытных данных (статистическое распределение выборки) состоит из N=Nm данных и имеет вид:

№ Измерения	Уровни фактора А
A1	A2	A3	…	Am
1	X11	X12	X13	…	X1m
2	X21	X22	X23	…	X2m
…	…	…	…	…	…
N	Xn1	Xn2	Xn3	…	Xnm
Групповые средние				…

В последней строке таблицы приведены средние значения величины Х для соответствующих уровней фактора А (групповые средние). Они подсчитываются как средние по каждому столбцу:

(4.3)

Общая средняя величины Х может быть найдена по формуле

(4.4)

Или проще, если найдены групповые средние (4.3):

(4.5)

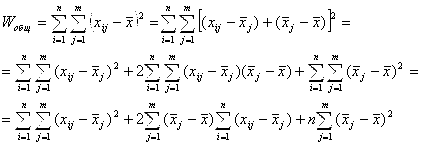
Рассмотрим теперь общий объем вариации (колеблемости) значений Xij величины Х вокруг ее общей средней :

(4.6)

Разложим, в соответствии с (4.1), WОбщ на WA И WОст:

(4.7)

Теперь учтем, что

(4.8)

И введем обозначения:

(4.9)

Тогда выражение (4.7) для WОбщ примет вид:

WОбщ=WA+WОст

(4.10)

Составляющая WA общей вариации WОбщ действительна связана с действием фактора А, так как она определяется разбросом групповых средних , соответствующих разным уровням фактора А, вокруг общей средней . И если фактор А действительно влияет на величину Х, то групповые средние будут существенно разными, и величина WA будет значительной. А если влияние фактора А несущественно, то групповые средние будут мало отличатся между собой, и WA будет малой. Впрочем, значительность или незначительность величины WA можно установить лишь путем сравнения ее с WОст, которая, очевидно, характеризует степень внутригруппового разброса значений . И сравниваются они следующим образом. На основании подсчитанных сумм WОбщ, WA И WОст находятся общая , факторная и остаточная дисперсии, которые вычисляются путем деления указанных сумм на соответствующее каждой из них число степеней свободы

(4.11)

Напомним (см. также §2), что число степеней свободы некоторой вычисляемой по опытным данным случайной величины – это количество этих данных, участвующих в ее формировании, за вычетом количества независимых друг от друга числовых характеристик, вычисляемых по тем же опытным данным и тоже участвующих в формировании указанной величины. Из сказанного и выражений для WОбщ, WA и WОст и следуют формулы (4.11).

Итак,

(4.12)

Теперь выдвинем нулевую гипотезу Н0 - фактор А несущественно (незначимо) влияет на величину Х при альтернативной гипотезе Н1, Что он на неё влияет существенно (значимо).

Если проверяемая гипотеза Н0 Справедлива, то найденные групповые средние должны несущественно (незначимо) отличаться друг от друга. То есть математические ожидания всех групповых средних должны быть одинаковы и равны общей средней . И будет это не так, если гипотеза Н0 несправедлива.

Для применимости дисперсионного анализа при проверке гипотезы Н0 должны выполняться Два обязательных условия:

1. Должны незначимо различаться все внутригрупповые дисперсии. То есть все остальные случайные (неучтенные) факторы на любом из уровней фактора А должны действовать на величину Х одинаково.

2. Величина Х должна иметь нормальное распределение на любом из уровней фактора А.

При выполнении этих условий для проверки гипотезы Н0 можно использовать критерий Фишера-Снедекора

(4.13)

Доказано (см. например [5], стр. 379-380), что при справедливости гипотезы Н0 (при незначимости фактора А) все три дисперсии (4.12) являются точечными несмещенными оценками генеральной дисперсии S2. То есть их математические ожидания равны S2:

(4.14)

А значит, при справедливости гипотезы Н0, факторная дисперсия должна быть приблизительно такой же, как и остаточная дисперсия . И тогда будет F » 1. Но если гипотеза Н0 неверна (фактор А значим для величины Х), то факторная дисперсия должна быть существенно больше остаточной, и тогда величина F должна быть существенно больше 1.

Доказано, что при указанных выше условиях и при справедливости гипотезы Н0 случайная величина F, определяемая формулой (4.13), распределена по закону Фишера-Снедекора со степенями свободы и . Поэтому для проверки гипотезы Н0 При заданном уровне значимости A достаточно с помощью таблицы критических точек распределения Фишера-Снедекора для данных значений (A; KА; kост) найти критическое значение FКр случайной величины F и сравнить его с экспериментальным значением FЭксп, подсчитанным по формуле (4.13). И если FЭксп>FКр то гипотезу Н0 отвергают. То есть считают, что фактор А существенно (значимо) влияет на величину Х, а значит, различие найденных групповых средних не случайно. А если FЭксп<FКр, то гипотезу Н0 принимают. То есть считают, что фактор А является незначимым – его влияние на величину Х в принципе такое же, как и влияние прочих неучтенных случайных факторов (помех). И значит, различие групповых средних – случайно.

Критерий Фишера-Снедекора позволяет установить наличие или отсутствие существенных (значимых) различий между групповыми средними В целом, однако он не показывает, между какими средними разница существенна, а между какими нет. Поэтому если проведенный дисперсионный анализ привел к отказу от нулевой гипотезы Н0, предполагающей равенство групповых средних, и показал, таким образом, существенность влияния проверяемого фактора А на величину Х, то этот общий вывод необходимо дополнить проверкой существенности различий между парами средних. Наиболее просто это сделать, сравнив модули всех разностей групповых средних с так называемой НСР – Наименьшей существенной разностью (см. [1], § 6.3):

(4.15)

Здесь TКр – критическое значение распределения Стьюдента для заданного уровня значимости A и числа степеней свободы . Разности, по модулю бóльшие НСР, считаются значимыми, меньшие – незначимыми.

Примечание 1. Формулы (4.7) и (4.9) не очень удобны для ручного подсчета сумм WОбщ, WА И WОст , что затрудняет подсчет общей, факторной и остаточной дисперсий (4.12). Но эти формулы можно и существенно упростить.

Во-первых, легко показать (проделайте это самостоятельно), что указанные формулы можно преобразовать к виду:

(4.16)

Где

(4.17)

Во-вторых, учтем, что замена Xij На Yij, определяемая равенствами

Yij =xij – C,

(4.18)

Где С – любая константа, не изменит, очевидно, ни одну из вариаций WОбщ, WA И WОст. При этом для упрощения счета удобно в качестве константы С взять число, близкое к общей средней , что позволит кардинально уменьшить числа Xij, если они велики. В итоге для WОбщ, WA И WОст получим окончательно:

(4.19)

Здесь

(4.20)

Все эти суммы легко вычисляются вручную.

Отметим еще, что при замене (4.18) Xij На Yij не изменятся, очевидно, и все разности между групповыми средними , которые заменятся на разности между групповыми средними . Поэтому выяснение вопроса о том, какие из разностей между значимы, а какие нет, можно заменить выяснением этого вопроса о разностях между .

Примечание 2. На практике не всегда удается гарантировать одинаковое количество N экспериментальных данных на каждом уровне Ai фактора А.

Пусть это количество Nj зависит от номера J уровня фактора. Тогда общий объем N выборки будет, очевидно, таков:

(4.21)

Формулы (4.19) для этого случая примут вид:

(4.22)

Здесь

(4.23)

Общая, факторная и остаточная дисперсии должны подсчитываться по тем же
формулам (4.12):

(4.24)

Формулы (4.13) и (4.15) и схемы их использования остаются без изменений.

Номер Измерения	Уровни фактора А
A1	A2	A3
1	151	152	142
2	152	154	144
3	156	156	150
4	157	158	152
Групповые средние	154	155	147

Пример 1. Исследовать влияние фактора А на случайную величину Х при указанной слева таблице экспериментальных данных. Предполагается, что выборки произведены из нормальных генеральных совокупностей с одинаковыми дисперсиями. Методом дисперсионного анализа при уровне значимости A = 0,05 проверить гипотезу Н0 О несущественности (незначимости) влияния данного фактора А на изучаемую величину Х.

Решение. Для упрощения расчетов вычтем некую среднюю варианту, скажем С = 152, из каждого наблюдённого значения:

Yij = Xij – 152

После этого составим необходимую для реализации формул (4.19) и (4.20) расчетную таблицу:

Номер Измерения	Уровни фактора А
A1	A2	A3
1	-1	1	0	0	-10	100
2	0	0	2	4	-8	64
3	4	16	4	16	-2	4
4	5	25	6	36	0	0
		42		56		168
	8		12		-20
	64		144		400

На основании результатов этой таблицы и формул (4.19) получаем:

После этого реализуем формулы (4.12):

Теперь сравним по критерию Фишера-Снедекора факторную и остаточную дисперсии. Для этого сначала по формуле (4.13) найдем экспериментальное значение FЭксп Случайной величины F:

Учитывая теперь, что число степеней свободы числителя знаменателя и имея в виду заданный уровень значимости
A = 0,05, по таблице критических точек распределения Фишера-Снедекора находим:

FКр = F(0,05; 2; 9) = 4,26

И так как оказалось, что FЭксп >FКр, то гипотезу Н0 О несущественности (незначимости) фактора А для рассматриваемой случайной величины Х Отвергаем. То есть признаём, что фактор А существенно (значимо) влияет на величину Х. Иначе говоря, различие групповых средних в целом не случайно, а вызвано изменением уровней (A1; A2; A3) влияющего на величину Х фактора А.

А теперь уточним, какие из групповых средних различаются значимо, а какие нет. Сначала найдем модули всех возможных разностей групповых средних:

После этого по формуле (4.15) найдем наименьшую существенную разность (НСР) этих групповых средних. Так как согласно таблице критических точек распределения Стьюдента (см. таблицу 4 Приложения) TКр = TКр (0,05; 9) = 2,26,

То

Как видим, лишь модули разностей превышают наименьшую существенную разность НСР = 6,6, а модуль разности ее не превышает. То есть существенно (значимо) различаются лишь групповые средние .

Упражнения.

1. По выборочным данным, представленным в таблице

Номер Измерения	Уровни фактора А
A1	A2	A3	A4	A5	A6	A7
1	75	104	96	92	76	92	89
2	86	89	88	89	89	87	85
3		92	105		90	88	93
4		90	90		77	82
5		81	91		75	90
6						86
Групповые средние	80,5	91,2	94	90,5	81,4	87,5	89

При уровнях значимости а) A = 0,05 и б) A = 0,01 проверить гипотезу Н0 О незначимости влияния фактора А на изучаемую величину Х. Представить расчетную таблицу и результаты расчета для Yij = Xij – 88.

Ответ. В расчетной таблице должен быть осуществлен подсчет величин, фигурирующих в формулах (4.21) – (4.24):

Номер Изме- Рения	Уровни фактора А
A1	A2	A3	A4	A5	A6	A7
1	-13	169	16	256	8	64	4	16	-12	144	4	16	1	1
2	-2	4	1	1	0	0	1	1	1	1	-1	1	-3	9
3			4	16	17	289			2	4	0	0	5	25
4			2	4	2	4			-11	121	-6	36
5			-7	49	3	9			-13	169	2	4
6											-2	4
Pj		173		326		366		17		439		61		35	1417
Tj	-15		16		30		5		-33		-3		3		3
	112,5		51,2		180		12,5		217,8		1,5		3		578,5

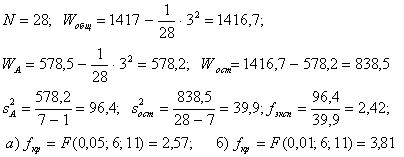
При обоих уровнях значимости а) A = 0,05 и б) A = 0,01 нет оснований отвергать гипотезу Н0 О незначимости влияния фактора А на исследуемую величину Х – гипотеза Н0 Принимается.

2. Подтвердить итоговые результаты предыдущего упражнения, если положить Yij = Xij – 90.

< Предыдущая		Следующая >