05. Размещения

Рассмотрим непустое конечное множество , .

1.) Из элементов этого множества сформируем различные выборки Без возвращения и с учётом порядка извлечённых элементов. Получаемые при таких условиях упорядоченные выборки называются Размещениями из элементов по элементов.

Число размещений для данного множества обозначается и вычисляется по формуле

.

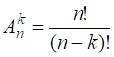Пример. Два студента сдают экзамен по математике. Сколько всего существует вариантов распределения оценок, если известно, что оба они сдали экзамен и получили разные оценки?

Решение. По условию задачи оба студента экзамен сдали. Поэтому данное множество оценок , , . Для ответа на вопрос задачи надо составить комбинаторные конфигурации из двух элементов множества без возвращения и с учётом порядка извлечённых элементов. Число вариантов распределения оценок в соответствии с заданными условиями равно числу размещений из 3 по 2 элементов:

.□

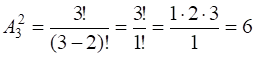2) Из элементов множества А сформируем различные выборки С возвращением и с учётом порядка извлечённых элементов. Получаемые при таких условиях упорядоченные выборки называются Размещениями С повторениями из элементов по элементов. Возможно, что больше .

Число размещений с повторениями для данного множества обозначается и вычисляется по формуле .

Пример. Два студента сдают экзамен по математике. Сколько всего существует вариантов распределения оценок, если известно, что оба они сдали экзамен?

Решение. По условию задачи оба студента экзамен сдали. Поэтому данное множество оценок , , . Для ответа на вопрос задачи надо составить комбинаторные конфигурации из двух элементов множества с возвращением и с учётом порядка извлечённых элементов. Число вариантов распределения оценок в соответствии с заданными условиями равно числу размещений с повторениями из 3 элементов по 2 элементов: .□

Задачи и упражнения.

5.1. Сколько всего различных двузначных чисел можно составить, используя цифры 1, 3, 5. Составьте все эти числа.

5.2. Сколько двузначных чисел можно составить, используя цифры 1, 3, 5, при условии, что цифры в записи числа не повторяются. Составьте все эти числа.

5.3. В первом семестре студенты изучают 11 дисциплин. В понедельник у студентов 4 пары, все по разным дисциплинам. Сколькими способами можно составить расписание на понедельник?

5.4. Сколько различных шестизначных телефонных номеров можно составить из четных цифр?

5.5. Сколько шестизначных чисел, кратных пяти, можно составить из цифр 1, 2, 3, 4, 5, 6 при условии, что цифры в числе не повторяются?

5.6. Докажите, что .

5.7. Вычислите, .

5.8. В университете учатся 1100 студентов. Докажите, что среди студентов университета обязательно найдутся хотя бы два человека с одинаковыми инициалами имени и фамилии.

< Предыдущая		Следующая >