Приложение 1 - Примеры решения задач и комментарии
Пример 1. Даны два вектора 
{3, 1, –5} и 
{6, –3, 0}. Найти сумму и разность этих векторов
= + и 
= –.
Решение. Найдем координаты векторов и .
Xc = 3+6= 9; Yc = 1 – 3= – 2; Zc = – 5+0 = – 5;
Xd = 3 – 6 = – 3; Yd = 1 – (–3) = 4; Zd = –5 – 0 = –5.
Ответ: {9, –2, –5}, { –3, 4, –5}.
Пример 2. Даны два вектора {3, 1, –5} и {6, –3, 0}. Найти линейную комбинацию этих векторов 
= 2
+3 
.
Решение. Найдем координаты вектора .
Xc = 
; Yc =
; Zc = 
;
Ответ. {24, –7, –10}.
Пример 3. Даны три вектора {1, 1, –2}, {2, –1, 0} и 
. Найти тот вектор, модуль которого будет наибольшим.
Решение. найдем модули трех векторов: 
;
; 
.
Ответ. Наибольший модуль у вектора 
.
Пример 4. Даны два вектора {1, 1, –2} и {2, –1, 0}. Найти косинус угла между векторами = 2 – и 
= + .
Решение. Найдем координаты векторов и .
Xc = 2 ´ 1 – 2 = 0; Yc = 2 ´ 1 – (–1) = 3; Zc = 2 ´ (–2) – 0 = -4;
Xd = 1 + 2 = 3; Yd = 1 + (–1) = 0; Zd = –2 + 0 = –2.
Итак: {0, 3, –4}, {3, 0, –2}.
Вычислим модули этих векторов и их скалярное произведение:
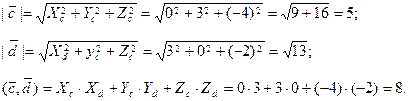
Теперь можно вычислить косинус угла J между этими векторами:
.
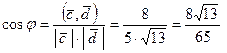Пример 5. При каком значении 
векторы – и a + ортогональны? (Координаты векторов и заданы в примере 4.)
Решение. Найдем координаты векторов – и a + :
;
.
Запишем условие ортогональности полученных векторов:
,
Или –a – 2 + 2a – 2 + 4a = 0.
После преобразования получим 5a – 4 = 0 ; откуда 
.
Пример 6. Вычислить определитель третьего порядка
.
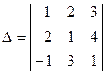Способ 1. Разложив определитель по первой строке, получим
Способ 2. Вычислим теперь тот же определитель, используя свойства определителя.
К элементам второй строки прибавим соответствующие элементы первой, умноженные на
(–2), а к элементам 3-й строки прибавим элементы первой строки, первую строку оставим без изменения (определитель не изменится):
.
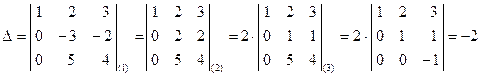Здесь произведены следующие действия: (1) – ко 2-й строке прибавили 3-ю; (2) – общий множитель второй строки вынесли за знак определителя; (3) – к 3-й строке прибавили 2-ю, умноженную на (–5). В результате получили определитель, под главной диагональю которого стоят нули (определитель верхней треугольной матрицы). Такой определитель равен произведению элементов главной диагонали (можно разложить по первому столбцу). Итак, мы вновь получили тот же ответ D = –2.
Этот способ выгодно использовать при вычислении определителей порядка N > 3.
Пример 7. Решить систему уравнений методом Крамера
.
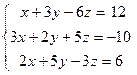Решение. Выпишем определитель системы и вектор-столбец правых частей:
.
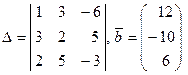Вычислим теперь определители D, D1, D2, D3.
.
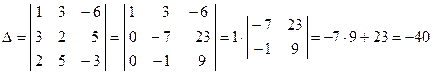Поясним проделанные вычисления. Из второй строки определителя мы вычли первую строку, умноженную на 3. В результате получили вторую строку нового определителя. Затем из третьей строчки определителя вычли первую строку, умноженную на 2. В результате получили третью строку нового определителя. Полученный новый определитель разложен по первой строке.
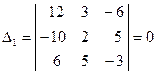, здесь определитель равен нулю, так как элементы первого столбца пропорциональны соответствующим элементам 3-го столбца.
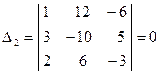, так как элементы второго столбца пропорциональны элементам третьего столбца.
.
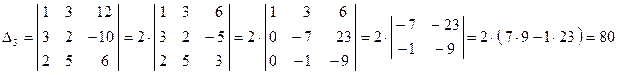Так как элементы третьего столбца являются четными числами, то мы вынесли число 2 за знак определителя. Далее из второй строки мы вычли элементы первой строки, умноженные на 3, а из элементов третьей строки вычли элементы первой строки, умноженные на 2. Величина определителя при этих преобразованиях не изменяется. В результате мы получили определитель, у которого в первом столбце стоят два нуля, и этот определитель можно вычислить путем разложения по первому столбцу.
Теперь, по правилу Крамера найдем решение системы:
Полезно сделать проверку, подставив решение в исходную систему. Проделав выкладки, легко убедиться, что решение найдено верно.
Пример 8. При каком значении С равен нулю определитель 
?
Решение. Выпишем определитель 
. По условию задачи
. Отсюда следует, что 
.
Пример 9. Во сколько раз изменится определитель матрицы третьего порядка, если все его элементы увеличить в два раза?
Решение. Если все элементы матрицы увеличить в два раза, то из каждой строки матрицы можно за знак определителя вынести число 2. Так как таких строк три, то определитель исходной матрицы увеличится в 
раз.
Пример 10. Вычислить определитель матрицы А =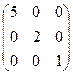 
.
Решение. Так как все элементы определителя, кроме элементов главной диагонали, равны нулю, то определитель равен произведению членов, стоящих на главной диагонали. Это следует как из общего правила вычисления определителя, так и из разложения определителя по первой строке (или по первому столбцу).
Ответ: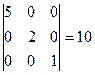 
.
Пример 11. Вычислить определитель матрицы А =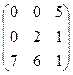 
.
Решение. Так как все элементы определителя, расположенные выше элементов побочной диагонали, равны нулю, то определитель равен произведению членов, стоящих на побочной диагонали, причем этот член будет входить в определитель со знаком минус. Это следует как из общего правила вычисления определителя, так и из разложения определителя по первой строке (или по первому столбцу).
Ответ: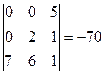 
.
Пример 12. Вычислить определитель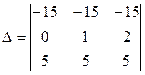 
.
Решение. Так как все элементы определителя, расположенные в первой строке, пропорциональны элементам третьей строки, то определитель равен нулю.
Пример 13. Вычислить определитель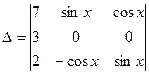 
.
Решение. Поскольку во второй строке определителя имеется только один ненулевой член, имеет смысл разложить определитель по элементам второй строки. В результате получим
.
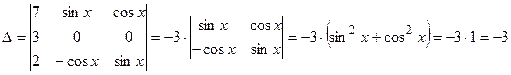На последнем шаге мы воспользовались основным тригонометрическим тождеством.
Пример 14. Матрица А равна А = 
. Написать матрицу, составленную из алгебраических дополнений 
( i=1,2; j = 1,2) исходной матрицы.
Решение. Напомним, что алгебраическим дополнением элемента 
называется число 
, где 
– минор элемента , а минором элемента матрицы А называется определитель Mij, полученный из матрицы А путем вычеркивания из матрицы i-ой строки и j-го столбца. В нашем случае для элемента 
алгебраическим дополнением будет 
, для элемента 
алгебраическое дополнение равно 
, для 
алгебраическое дополнение равно 
(знак минус написан потому, что для этого элемента сумма номера строки и столбца – нечетное число), для 
алгебраическое дополнение 
.
Ответ: матрица алгебраических дополнений для исходной матрицы имеет вид 
.
Пример 15. Для матрицы А =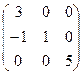 
написать матрицу, составленную из ее алгебраических дополнений.
Решение. Выпишем алгебраические дополнения для каждого элемента матрицы. В данном случае алгебраическими дополнениями будут определители второго порядка.
; 
; 
.
; 
; 
.
; 
; 
.
Знаки алгебраических дополнений определяются по правилу, описанному в предыдущем примере.
Ответ: матрица алгебраических дополнений имеет вид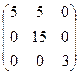 
.
Пример 16. Вычислить определитель 4-го порядка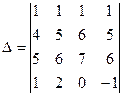 
.
Решение. При внимательном рассмотрении элементов определителя можно заметить, что каждый элементы третьей строки равен сумме соответствующих элементов первой и второй сроки. По разобранном в разделе 1.4 свойствам определителя это означает, что рассматриваемый определитель равен нулю.
Пример 17. Определить, при каких значения переменной 
верно следующее неравенство
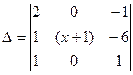<0 ?
Решение. Для решения задачи необходимо выразить определитель как функцию переменной и решить полученное неравенство. В данном случае удобно к первой строке определителя прибавить элементы третьей строки, после чего в первой строке останется только один ненулевой элемент.
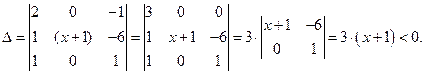
Полученное неравенство справедливо при 
.
Ответ: .
| < Предыдущая |
|---|
