09.1. Примеры
Пример 1. Новый продукт Московского часового завода. Конструкторское бюро Московского часового завода (МЧЗ) разработало новый настольный радиобудильник. По мнению проектировщиков, запуск в серию нового продукта позволит расширить рынок сбыта и получить дополнительную прибыль.
Руководство МЧЗ решило изучить возможности реализации нового продукта. Результатом исследования должны стать рекомендации относительно действий, которые следует предпринять для организации производства и сбыта нового продукта. Перечень работ и характеристики времени их выполнения (в неделях) указаны в следующей таблице:
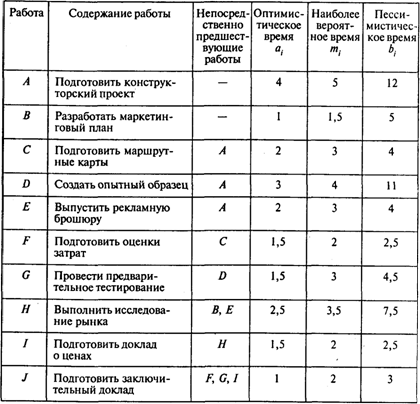
Вопросы:
1. Чему равен критический путь для данного проекта?
2. Чему равно ожидаемое время выполнения проекта?
3. С какой вероятностью проект может быть выполнен за 20 недель?
Решение. На рис. 1 показано графическое представление этого проекта.

Рис. 1
1-й способ решения. Используя информацию, указанную в условии, определяем ожидаемое время и вариацию времени выполнения каждой работы проекта. Например, для работы А:
![]()
Проводя аналогичные расчеты для других работ, получаем следующую таблицу:
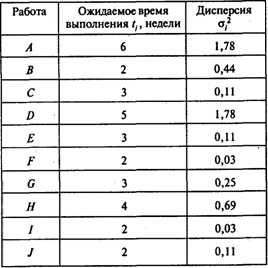
Полагая время выполнения работы равным ожидаемому времени ее выполнения Ti, находим критический путь. Используем для этого метод СРМ В виде следующей таблицы с указанием предшествующих работ:
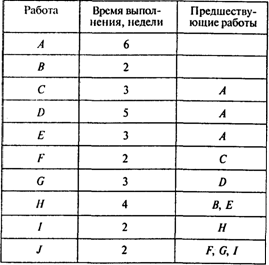
Результаты расчетов представлены в следующей таблице:
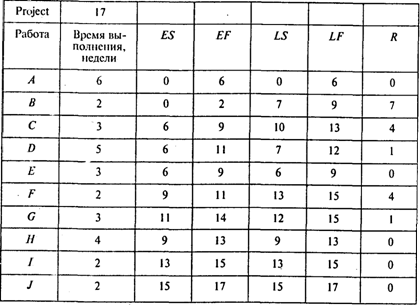
Критический путь для данного проекта включает работы А, Е, Н, I, J. Длина критического пути равна 6+3+4+2+2=17. Это означает, что ожидаемое время выполнения проекта составляет 17 недель.
Предполагая, что распределение времени выполнения проекта является нормальным, можно определить вероятность того, что проект будет выполнен за 20 недель.
Определим дисперсию времени выполнения проекта. Ее значение равно сумме значений дисперсий времени выполнения работ на критическом пути:
S2(T) = 1,78 + 0,11 + 0,69 + 0,03 + 0,11 = 2,72.
Учитывая, что ![]() находим значение Z для нормального распределения при T0 = 20:
находим значение Z для нормального распределения при T0 = 20:
![]()
Используя таблицу нормального распределения (Приложение 1), находим вероятность того, что время Т выполнения проекта находится в интервале Е(T) £ T £ Т0. На пересечении строки «1,8» и столбца «0,02» таблицы нормального распределения находим значение 0,4656. Следовательно, искомая вероятность того, что время Т выполнения проекта удовлетворяет условию Т £ 20, т. е. вероятность того, что проект будет выполнен за 20 недель при ожидаемом времени его выполнения 17 недель, равна 0,5 + 0,4656 = 0,9656.
2-й способ решения. Исходные данные представлены в следующей таблице (оценки времени выполнения работ указаны в неделях):
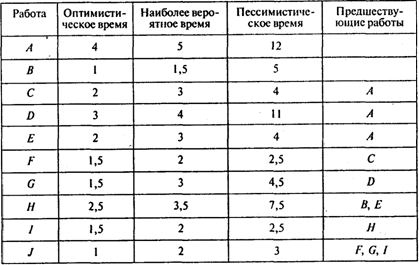
Проводя расчеты, получаем следующие результаты:
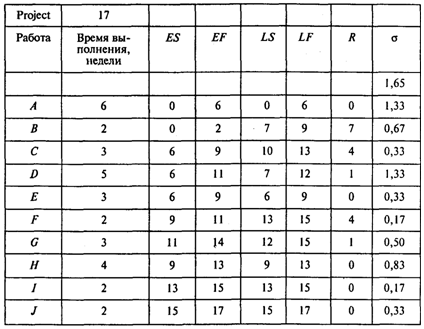
Последний столбец таблицы содержит значения стандартных ошибок времени выполнения проекта в целом (первое значение s(Т) = 1,65) и всех его работ в частности.
Так же, как в первом способе, находим значение Z для нормального распределения при Т0 = 20:
![]()
Используя таблицу нормального распределения (см. Приложение 1), находим вероятность того, что время T выполнения проекта находится в интервале Е(T) £ Т £ Т0. На пересечении строки «1,8» и столбца «0,02» таблицы нормального распределения находим значение 0,4656. Следовательно, искомая вероятность того, что проект будет выполнен за 20 недель при ожидаемом времени его выполнения 17 недель, равна 0,5 + 0,4656 = 0,9656.
Ответы:
1. Критический путь составляют работы А, Е, Н, I, J.
2.17 недель. 3. 0,9656.
| < Предыдущая | Следующая > |
|---|