04. Степень вершины графа

Рассмотрим граф , Имеющий P вершин и Q ребер.

Определение. Степенью вершины графа называется число ребер, инцидентных этой вершине .

Теорема.5. Степень любой вершины графа удовлетворяет неравенству .

Определение. Изолированной называется такая вершина графа, степень которой .

Определение. Концевой, или висячей, называется такая вершина графа, степень которой .

Теорема 6. (Теорема Эйлера.) Сумма степеней всех вершин графа равна удвоенному числу его рёбер: .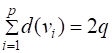

Например, для графа на рис. 1 степени его вершин , , , . Изолированных и концевых вершин в графе нет. Число ребер графа . По теореме Эйлера .

Следствием теоремы Эйлера является Лемма о рукопожатиях – сумма степеней всех вершин графа есть чётное число.

Название леммы интерпретируется так: вершины графа – это люди, а ребра – рукопожатия двух людей. При Любом числе рукопожатий общее число пожатых рук всегда чётное.

Задачи и упражнения

12. Определите степени вершин графа задачи 1. Укажите концевые и изолированные вершины.

13. В здании имеется 15 телефонных аппаратов. Докажите, что их нельзя соединить проводами так, чтобы каждый аппарат был соединен ровно с пятью другими.

14. В некотором государстве имеется 100 городов. Каждый город соединяется дорогами с пятью другими городами. Установите, сколько всего дорог в этом государстве.

15. На втором курсе института обучаются 253 студента. Одни из них знакомы, другие – не знакомы друг с другом. Докажите, что хотя бы у одного студента имеется чётное число знакомых среди студентов второго курса.

16. Для графа сформулируйте свойство вершин нечетной степени.

< Предыдущая		Следующая >