01. Определение неориентированного графа

Рассмотрим конечное Непустое множество мощности и множество мощности двухэлементных подмножеств множества .

Определение. Неориентированным графом , или , называется пара множеств и .

Элементы множества называются Вершинами Графа , элементы множества – его Ребрами. Ребро, соединяющее две различные вершины графа или, что то же самое, , обозначается . Ребра графа нумеруются Вне Зависимости от номеров соединяемых вершин. Указание множества вершин и множества ребер является Аналитическим способом задания графа.

Теорема.1. Любое множество двухэлементных подмножеств множества является симметричным бинарным отношением на множестве .

В силу теоремы 1 для множества выполняются свойства: и . Поэтому всякий элемент обозначается или, что то же самое, . Таким символом в теории графов обозначается двухэлементное множество .

Списком ребер графа называется перечень его ребер с указанием соединяемых вершин.

Определение. Инцидентной ребру называется каждая из концевых вершин этого ребра. Ребро называется Инцидентным своим концевым вершинам.

Определение. Смежными называются два ребра, инцидентные одной вершине.

Определение. Смежными Называются две вершины, инцидентные одному ребру.

Определение. Диаграммой называется изображение графа в виде точек и линий.

Диаграмма является Геометрическим способом задания графа.

Например, на рис. 1 приведена диаграмма графа , имеющего четыре вершины и пять ребер.

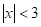
Рис. 1. Диаграмма графа

Множеством вершин графа является множество . Множеством ребер графа является множество с элементами , , , , . В этом графе вершины , , , , являются смежными; ребра , , , , , , , – смежными.

В этом графе вершины являются несмежными, ребра , – несмежными.

Определение. Подграфом графа называется граф , для которого или .

Факт, что является подграфом графа , обозначается .

Определение. Подграф называется Остовным подграфом , если .

Определение. Подграф называется Собственным подграфом , если и .

Определение. Подграф называется Правильным подграфом , если .

Например, на рис. 2 представлены диаграммы подграфов графа, изображенного на рис. 1.

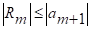
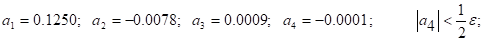
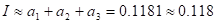
А) Б) В)

Рис. 2. Диаграммы подграфов: А – остовной; Б – собственный; В – правильный

Определение. Петлей графа называется элемент множества E, состоящий из одинаковых элементов множества V. Граф с петлей называется Псевдографом.

Определение. Кратными ребрами графа называется набор одинаковых элементов множества E. Граф с кратными ребрами называется Мультиграфом.

Определение. Гиперграфом называется граф, для которого множество Е состоит из троек, четверок, …, P-ок элементов множества V.

Определение. Помеченным называется граф с дополнительно заданной функцией или . Множество М называется Множеством пометок.

Далее рассматриваются неориентированные непомеченные графы без петель и кратных ребер.

Допускается обозначение вершин на диаграмме графа натуральными числами от 1 до P или только точками.

Задачи и упражнения

1. Запишите множества V и E, определите числа P и Q, укажите все пары смежных вершин графов, заданных следующими диаграммами:

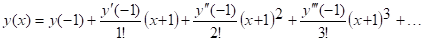
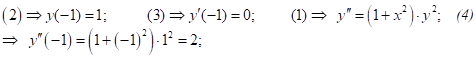
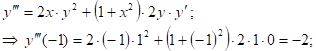
2. Задайте графы задачи 1 списком ребер. Укажите все пары смежных ребер.

3. Выделите остовной, собственный и правильный подграфы графов задачи 1.

4. Постройте диаграммы следующих графов, имеющих 5 вершин и заданных списками ребер:

1) , , , ;

2) , , , , , , , .

Следующая >