20. Свойства сходящихся рядов

Необходимый признак сходимости ряда. Если сходится, то An®0 .

Доказательство. У сходящегося ряд сходится последовательность частичных сумм {Sn}Þ "e>0 $ N(e ): |Sn+m-Sn|<e для " N>N и "M>0 Þ |An+1|=|Sn+1-Sn|<e для "N>NÞ An®0 при N®¥.

Теорема 9.1. Пусть C – комплексное число. Если ряд сходится, то и ряд Также сходится и

.

Доказательство. Рассмотрим частичные суммы и . По условию $. Т. к. Sn=CS’N И =. Согласно определению суммы ряда отсюда сразу следует

.

Теорема 9.2. Пусть ряды и сходятся, тогда ряд также сходится и

=+.

Доказательство. Рассмотрим частичные суммы , и . Очевидно, sN=Sn+S’N. По условию $ и Þ $= +. Откуда сразу следует утверждение теоремы.

Пример. ==.

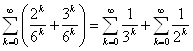< Предыдущая		Следующая >