03. Тригонометрическая и показательная формы записи комплексного числа

Перейдя на комплексной плоскости к полярным координатам

(X,Y) <=> (r, j), где X=r cos j, Y=r sin j, получим Тригонометрическую форму записи комплексного числа z=r (cosj +ISinj )

Здесь
r =(X2+Y2)1/2=ïZï =((Re Z)2+(Im Z)2)1/2 - Модуль комплексного числа,

Tg j =Y/X; j =j0+2p K- Аргумент комплексного числа.

Arg Z=arg Z+2p K, 0 arg Z <2p.

Для комплексного числа 0=(0,0) модуль равен 0, а аргумент не определен.

Тригонометрическую и показательную форму записи комплексного числа связывает Формула Эйлера

Z=r (cosj +ISinj )=r EiJ

Эта формула определяет экспоненту в мнимой степени (ее не нужно доказывать).

Примеры

1. Z=1: |1|=1, arg 1=0; 1=1(cos 0 +I sin 0)= 1eI0;

2. Z=I: |I|=1, arg I=p /2; I=1(cos p /2 +I sin p /2)= 1eIP /2;

3. Z=-1: |-1|=1, arg (-1)= p ; -1=1(cos p +I sin p )= 1eIP ;

4. Z=-I: |-I|=1, arg (-I)= 3p /2; -I=1(cos 3p /2 +I sin 3p /2)= 1eI3p /2;

5. Z=1+I: |1+I|=, arg (1+I)= p /4; 1+I= (cos p /4 +I sin p /4)= eIP /4;

6. Z=eIJ; |eIJ |=1, arg (eIJ)= j ; eIJ=1 (cos j +I sin j );

7. Z=-eIJ; |-eIJ |=1, arg (-eIJ)= p +j ; - eIJ=1 (cos(p +j ) +I sin(p +j ))=eI(p +j )

Геометрическая интерпретация сложения и умножения.

Сложение двух комплексных чисел можно рассматривать как сложение двух векторов на плоскости. При этом выполнено:

Неравенство треугольника

ïZ1+Z2ïïZ1ï+ïZ2ï.

В частности ïA+IbïïAï+ïBï

ïZ1-Z2ï - Расстояние между Z1 и Z2 на комплексной плоскости.

Простейшие множества точек на комплексной плоскости.

А) |z-z0|=a (a>0) - окружность с центром в точке z0 радиуса A;

Б) |z-z0|<a (a>0) - открытый круг с центром в точке z0 радиуса A;

В) |z-z0|>a (a>0) - внешность открытого круг с центром в точке z0 радиуса A;

Г) A<|z-z0 |<b (0<a<b) - открытое кольцо с центром в точке Z0;

Д) arg(Z-z0)= j - луч, с началом в точке Z0 , идущий под углом j к положительному направлению действительной оси.

Е) a <arg(Z-z0)<b - внутренность неограниченного открытого сектора с вершиной в точке Z0 и углом раствора b - a.

Ж) Re Z= a - прямая, || мнимой оси, проходящая через точку (A,0);

З) Im Z= b - прямая, || действительной оси, проходящая через точку (0,B);

При Умножении двух комплексных чисел их Модули перемножаются (растяжение или сжатие), а Аргументы складываются (поворот на плоскости).

Z1=A1+I b1=r1eIA; Z2=A2+I b2=r2eIB;

Z1·Z2=r1r2ei(a +b ) => |Z1Z2|=|Z1||Z2|; arg(Z1 Z2)=arg Z1+ arg Z2 .

При Делении двух комплексных чисел их Модули делятся (модуль знаменателя ¹ 0), а Аргументы вычитаются

Z1/Z2=(r1/r2)eI(a - b )=> |Z1/Z2|=|Z1|/|Z2|; arg(Z1/Z2)=arg Z1- arg Z2 .

Алгебраической формой записи комплексных чисел удобно пользоваться при операциях сложения и вычитания, а показательной - при умножении, делении, возведении в целую степень, извлечении целого корня (возведение в рациональную степень).

Возведение в целую степень.

ZN=[r(cosj +I sinj)]n=[r eIJ ]n =rneINj=r n(cos(nj)+I sin(nj));

Мы вывели

Формулу Муавра: (cosj +I sinj )n = cos(nj )+I sin(nj ).

Пример: (1+I)3=(21/2 eIP /4)3=23/2 Ei3P /4=23/2(cos(3p /4)+I sin(3p /4))=-2+2I.

Извлечение целого корня (возведение в рациональную степень).

Z n =r eIJ= r eI(J +2p k) , k=0, 1, 2... .

Z =r 1/n eI(J +2p k)/n.

=> корень N-ой степени имеет N различных значений, которые получаются при K=0, 1, 2...,N-1.

Пример: =1 eI(0+2p k)/4=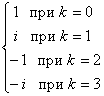

2. Последовательности комплексных чисел.

Определение. Последовательностью комплексных чисел называют упорядоченное счетное множество комплексных чисел {ZN}

Определение. Комплексное число Z называется Пределом последовательности {ZN}, если для " e >0 $ N(e ): ïZn-zï <e для " n> N.

{zn}® z; zn=z.

Примеры.

А) z/n=0;

Б) Arg[(-1)n/n] не $,

Arg[(-1)n/n]=0 при четных n,

Arg[(-1)n/n]=p при нечетных n.

Задание комплексной последовательности ZN=AN+IbN : {ZN}={AN}+I{BN}- одновременное задание двух действительных последовательностей.

Теорема 1.1. Необходимым и достаточным условием {ZN}® Z= A+Ib Является требование {AN}® A; {bn}® B.

Доказательство.
Необходимость.

"e>0 $ N(e ): ïZN-Zï<e для " n >N Þ

ïAN-AïïZN-Zï<e,ïBN-BïïZN-Zï <e Þ {AN}® A, {BN}® B.

Достаточность.

"e >0 $ N1(e ): ïAN-Aï <e /2 для " n>N1,

$ N2(e): ïBN-Bï<e /2 для " n>N2 Þ

$ N=max{N1,N2}: ïZN-ZïïAN-Aï+ïBN-Bï<e для " n> N. n

Определение. Последовательность {ZN} называется Ограниченной, если $ AÎReal: " N ïZnï<A.

Любая сходящаяся последовательность ограничена.

Критерий Коши. Необходимым и достаточным условием сходимости {zN}® z является требование, чтобы для " e >0 $ N(e): ïZn+m-Znï<e для " n>N и " m>0.

Доказательство.

Необходимость.

{ZN}® z (ZN= AN+IbN ) Þ{AN}® A и {BN}® b Þ

" e >0 и " m>0 $ N1(e):ïAN+m-ANï<e/2 для " n>N1(e)

И $ N2(e):ïBN+m-BNï<e/2 для " n>N2(e).Þ

$ N(e)= max{N1,N2}: ïZN+m-ZNï<e для " n>N(e)

Достаточность.
ïZN+m-ZNï<e для " n>N(e) Þ ïAN+m-ANï, ïBN+m-BNïïZN+m-ZNï<eÞ{AN}® A и {BN}® b n

Неограниченно возрастающие последовательности.

Определение. Если для " A>0 $ N(A): ïZNï>A для " n>N(A), то последовательность {ZN} называется Неограниченно возрастающей.

Примеры. а) ZN=ZN при |Z|>1; б) ZN= I n.

В обычном смысле неограниченные последовательности не сходятся, но оказывается удобным считать, что существует единственная Бесконечно удаленная точка комплексной плоскости. Все неограниченно возрастающие последовательности сходятся К этой единственной точке

ZN= z¥ =¥.

{xn=1/ZN}®0

1/ z¥ =0, 1/0=¥ , z·¥=¥ ( z¹0), z+¥ =¥ , z/¥ =0 (z¹¥). Операции 0/0 и ¥/¥ являются неопределенными.

< Предыдущая		Следующая >