01. Комплексные числа и действия над ними
Определение. Комплексным числом называется пара действительных чисел с установленным порядком следования Z=(a, b),
A=Re(z)- Действительная часть комплексного числа,
B=Im(z)- Мнимая часть.
Действительные числа включаются в множество комплексных чисел.
Примеры: A=(A,0) - вещественное число, (0,B) - чисто мнимое число,
(0,1)=I - мнимая единица.
0=(0,0), -1=(-1,0), -I=(0,-1).
Комплексные числа можно изображать точками на комплексной плоскости.
Действия с комплексными числами:
1) Равенство. Z1=Z2 Û A1=A2, B1=B2.
Операция сравнения Не определена!!!
2) Сложение. Z1+Z2=(A1+A2,B1+B2)
(A,0)+(0,B)=(A,B) – всякое комплексное однозначно разлагается на сумму чисто действительного и чисто мнимого чисел.
3) Умножение. ![]() .
.
B·I=(B,0)·(0,1)=(0,B).
Þ алгебраическая форма записи комплексного числа
Z =(A,0)+(0,B)= A + Ib = Re(Z) + I·Im(Z).
Пример: I·I=-1
Þ алгебраические операции с комплексными числами можно совершать, как с обычными многочленами, помня, что I2=-1.
Договоримся, всякий ответ доводить до алгебраической формы записи комплексного числа, если не оговорено обратное.
4) Комплексное сопряжение.
Z=(A, B)=A + Ib; Z* = (A, -B) = A - Ib.
Полезно: Re(Z) = ( Z + Z* ) / 2; Im(Z) = (Z - Z* ) / 2I.
Некоторые свойства.
A) (Z1 ± Z2)*= Z1* ± Z2*;
B) (Z*)* = Z;
C) z· z* = (A + Ib)(A - Ib) = A2 + B2ÎReal
Обратные операции.
5) Вычитание. Z1 - Z2 = (A1 - A2, B1 - B2).
6) Деление ![]()
Примеры. (2+I)/(1+2I)= (2+I)(1-2I)/(1+4)=0.8-0.6I;
1/I = -I.
7) Возведение в целую степень.
Примеры:
a) I2 = -1;
б)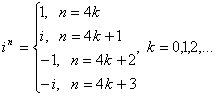
В) Z2 = (A+Ib)2 = A2 + 2Iab - B2 = (A2 - B2) + I 2Ab Þ ; Re(Z2)=(A2- B2), Im(Z2) = 2Ab.
| Следующая > |
|---|