6.5. Нормальный закон распределения

Нормальный закон распределения (закон Гаусса) играет исключительную роль в теории вероятностей. Главная особенность закона Гаусса состоит в том, что он является Предельным законом, к которому приближаются, при определенных условиях, другие законы распределения. Нормальный закон распределения наиболее часто встречается на практике.

Непрерывная случайная величина X имеет Нормальный закон распределения (закон Гаусса) с параметрами и , если ее плотность вероятности имеет вид:

.

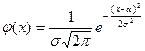Кривую нормального закона распределения называют Нормальной кривой или Кривой Гаусса.

Нормальная кривая изображена на рис. 9.

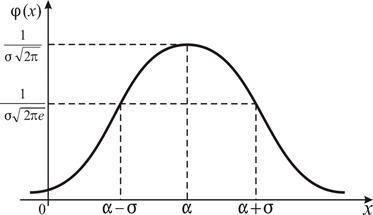
Рис. 9

Тот факт, что случайная величина X распределена по нормальному закону с параметрами , коротко записывают так: .

Математическое ожидание случайной величины X, распределенной по нормальному закону, равно параметру этого закона, т. е. , а дисперсия – параметру , т. е. .

Нормальный закон распределения случайной величины с параметрами и , т. е. случайной величины называется Стандартным или Нормированным.

Плотность стандартной случайной величины X имеет вид

И называется Функцией Гаусса.

Вероятность попадания в интервал (a, b) случайной величины X, подчиненной нормальному закону, определяется формулой

, (16)

Где функция 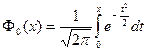называется Функцией Лапласа (или Интегралом вероятности). Эту функцию называют также Функцией ошибок.

Функция Лапласа обладает следующими свойствами:

1. , т. е. функция - нечетная;

2. ; 3. .

Таблицу значений функции Лапласа можно найти в приложении 1.

Вероятность попадания случайной величины в интервал , симметричный относительно центра рассеяния , находится по формуле

. (17)

В частности, , т. е. практически достоверно, что случайная величина принимает свои значения в интервале . Это утверждение называется “правилом трех сигм”.

< Предыдущая		Следующая >