§ 11. Гармонические колебания

Тригонометрические функции используются для описания различных колебательных процессов: колебания груза, подвешенного на пружине, вокруг положения равновесие, закон изменения переменного тока в цепи, колебания маятника, распространение звуковых и цветовых волн и т. д.

Формулы и , с помощью которых описываются такие процессы, называются формулами Гармонических колебаний. Положительная величина А называется Амплитудой колебания, положительная величина W – Частотой колебания, величина J – Начальной фазой колебания. Амплитуда характеризует размах колебания, частота – количество колебаний в единицу времени.

Построение графиков гармонических колебаний (гармоник) , производится в несколько этапов.

Рассмотрим алгоритм построения графика функции : а) строим график функции ; б) строим график функции , сдвигая график функции на |J| единиц по оси ОХ (если , то сдвигаем влево, если , то сдвигаем вправо); в) строим график функции , сжимая его в W раз к оси OY; г) строим график функции , растягивая его в A раз от оси ОХ.

Заметим, что функции и , описывающие гармонические колебания, являются периодическими с периодом . Они ограничены сверху и снизу, их наибольшее и наименьшее значения равны .

Пример 15. Постройте график гармонического колебания .

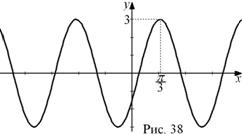Решение. Для этой гармоники амплитуда , частота – , начальная фаза – .

Строим график функции ; сдвигаем на единиц по оси ОХ вправо; сжимаем график к оси OY в 2 раза; растягиваем от оси OX В 3 раза (рис. 38).

Пример 16. Постройте график гармонического колебания .

Решение. Преобразуем формулу, раскрыв в аргументе косинуса скобки: . Следовательно, для этой гармоники амплитуда , частота – , начальная фаза – .

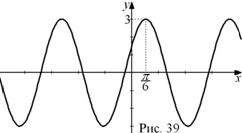Строим график функции ; сдвигаем график на единиц по оси ОХ вправо; сжимаем график к оси OY в 2 раза; растягиваем от оси OX В 3 раза (рис. 39).

Пример 17. Постройте график гармонического колебания .

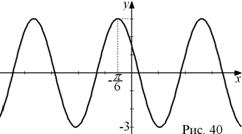Решение. Эта формула не задает гармоническое колебание, так как . Применив формулу приведения , преобразуем формулу к виду: . Следовательно, для этой гармоники амплитуда , частота – , начальная фаза – .