§ 04. Обратная функция
Пусть функция ![]() , определенная на множестве Х, такова, что любым двум различным значениям аргумента Х ставит в соответствие различные значения У, то есть, если
, определенная на множестве Х, такова, что любым двум различным значениям аргумента Х ставит в соответствие различные значения У, то есть, если ![]() , то
, то ![]() . Эта функция устанавливает взаимнооднозначное соответствие между областью своего определения Х и областью изменения Y.
. Эта функция устанавливает взаимнооднозначное соответствие между областью своего определения Х и областью изменения Y.
 Действительно, каждой точке
Действительно, каждой точке ![]() ставится в соответствие единственное
ставится в соответствие единственное ![]() . При этом каждой точке
. При этом каждой точке ![]() соответствует единственное
соответствует единственное ![]() , такое, что
, такое, что ![]() . Таким образом, на множестве Y определена функция
. Таким образом, на множестве Y определена функция ![]() , которая называется Обратной к функции F. Область определения обратной функции – множество Y, область значений – множество Х. Графики функции
, которая называется Обратной к функции F. Область определения обратной функции – множество Y, область значений – множество Х. Графики функции ![]() и обратной к ней функции
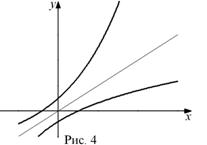
и обратной к ней функции ![]() симметричны относительно прямой
симметричны относительно прямой ![]() (рис. 4). Для обратных функций верно соотношение
(рис. 4). Для обратных функций верно соотношение ![]() .
.
Для нахождения обратной функции необходимо из равенства ![]() выразить Х через У, и в полученном выражении
выразить Х через У, и в полученном выражении ![]() букву Х заменить буквой У, букву У – буквой Х.
букву Х заменить буквой У, букву У – буквой Х.
Пример 3. Имеют ли функции ![]() и
и ![]() обратные? Если да, то найдите их.
обратные? Если да, то найдите их.
Решение. Выразим Х из формулы ![]() . Получим
. Получим ![]() . Обозначив аргумент через Х, а функцию через У, получим
. Обозначив аргумент через Х, а функцию через У, получим ![]() , то есть функция
, то есть функция ![]() является обратной к функции
является обратной к функции ![]() .
.
Функция ![]() не имеет обратной, так как она не является взаимнооднозначной. Действительно,
не имеет обратной, так как она не является взаимнооднозначной. Действительно, ![]() .
.
Пример 4. Являются ли функции ![]() и
и ![]() взаимнообратными?
взаимнообратными?
Решение. Нет, так как ![]() . Однако, если данные функции рассматривать только при
. Однако, если данные функции рассматривать только при ![]() , то есть считать
, то есть считать ![]() , то эти функции становятся взаимнообратными.
, то эти функции становятся взаимнообратными.
| < Предыдущая | Следующая > |
|---|