19. Моделирование сезонных колебаний

Простейший подход к моделированию сезонных колебаний – это расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда.

Общий вид аддитивной модели следующий:

. (4.3)

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (T), сезонной (S) и случайной (E) компонент.

Общий вид мультипликативной модели выглядит так:

. (4.4)

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (T), сезонной (S) и случайной (E) компонент.

Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.

Построение аддитивной и мультипликативной моделей сводится к расчету значений T, S и E для каждого уровня ряда.

Процесс построения модели включает в себя следующие шаги.

1) Выравнивание исходного ряда методом скользящей средней.

2) Расчет значений сезонной компоненты S.

3) Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных () в аддитивной или () в мультипликативной модели.

4) Аналитическое выравнивание уровней () или () и расчет значений T с использованием полученного уравнения тренда.

5) Расчет полученных по модели значений () или ().

6) Расчет абсолютных и/или относительных ошибок. Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок E для анализа взаимосвязи исходного ряда и других временных рядов.

Методику построения каждой из моделей рассмотрим на примерах.

Пример. Построение аддитивной модели временного ряда.

Обратимся к данным, представленным в табл. 4.1.

Было показано, что данный временной ряд содержит сезонные колебания периодичностью 4, т. к. объем потребления электроэнергии в первый-второй кварталы ниже, чем в третий-четвертый. Рассчитаем компоненты аддитивной модели временного ряда.

Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:

1.1. Просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объемы потребления электроэнергии (гр. 3 табл. 4.5).

1.2. Разделив полученные суммы на 4, найдем скользящие средние (гр. 4 табл. 4.5). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.

1.3. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр. 5 табл. 4.5).

Таблица 4.5

№ квартала, T	Объем потребления Электроэнергии,	Итого за Четыре квартала	Скользящая средняя За четыре квартала	Центрированная Скользящая Средняя	Оценка Сезонной Компоненты
1	2	3	4	5	6
1	375	–	–	–	–
2	371	2630	657,5	–	–
3	869	2612	653	655,25	213,75
4	1015	2712	678	665,5	349,5
5	357	2835	708,75	693,75	‑336,75
6	471	2840	710	709,375	‑238,375
7	992	2873	718,25	714,125	277,875
8	1020	2757	689,25	703,75	316,25
9	390	2757	689,25	689,25	‑299,25
10	355	2642	660,5	674,875	‑319,875
11	992	2713	678,25	669,375	322,625
12	905	2812	703	690,625	214,375
13	461	2740	685	694	‑233
14	454	2762	690,5	687,75	‑233,75
15	920	–	–	–	–
16	927	–	–	–	–

Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр. 6 табл. 4.5). Используем эти оценки для расчета значений сезонной компоненты S (табл. 4.6). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты . В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.

Для данной модели имеем:

.

Корректирующий коэффициент: .

Рассчитываем скорректированные значения сезонной компоненты () и заносим полученные данные в таблицу 4.6.

Проверим равенство нулю суммы значений сезонной компоненты:

.

Шаг 3. Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины (гр. 4 табл. 4.7). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.

Шаг 4. Определим компоненту T данной модели. Для этого проведем аналитическое выравнивание ряда () с помощью линейного тренда. Результаты аналитического выравнивания следующие:

.

Подставляя в это уравнение значения , найдем уровни T для каждого момента времени (гр. 5 табл. 4.7).

Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням T значения сезонной компоненты для соответствующих кварталов (гр. 6 табл. 4.7).

На одном графике отложим фактические значения уровней временного ряда и теоретические, полученные по аддитивной модели.

Таблица 4.7

T				T
1	2	3	4	5	6	7	8
1	375	‑292,448	667,448	672,700	380,252	‑5,252	27,584
2	371	‑266,781	637,781	673,624	406,843	‑35,843	1284,721
3	869	268,636	600,364	674,547	943,183	‑74,183	5503,117
4	1015	290,593	724,407	675,470	966,063	48,937	2394,830
5	357	‑292,448	649,448	676,394	383,946	‑26,946	726,087
6	471	‑266,781	737,781	677,317	410,536	60,464	3655,895
7	992	268,636	723,364	678,240	946,876	45,124	2036,175
8	1020	290,593	729,407	679,163	969,756	50,244	2524,460
9	390	‑292,448	682,448	680,087	387,639	2,361	5,574
10	355	‑266,781	621,781	681,010	414,229	‑59,229	3508,074
11	992	268,636	723,364	681,933	950,569	41,431	1716,528
12	905	290,593	614,407	682,857	973,450	‑68,450	4685,403
13	461	‑292,448	753,448	683,780	391,332	69,668	4853,630
14	454	‑266,781	720,781	684,703	417,922	36,078	1301,622
15	920	268,636	651,364	685,627	954,263	‑34,263	1173,953
16	927	290,593	636,407	686,550	977,143	‑50,143	2514,320

Рис. 4.6.

Для оценки качества построенной модели применим сумму квадратов полученных абсолютных ошибок.

.

Следовательно, можно сказать, что аддитивная модель объясняет 97% общей вариации уровней временного ряда по кварталам за 4 года.

Шаг 6. Прогнозирование по аддитивной модели. Предположим, что по нашему примеру необходимо дать прогноз об общем объеме потребления электроэнергии на I и II кварталы 2003 года. Прогнозное значение уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда

.

Получим

;

.

Значения сезонных компонент за соответствующие кварталы равны: и . Таким образом,

;

.

Т. е. в первые два квартала 2003 г. следовало ожидать объема потребления электроэнергии порядка 395 и 422 кВт соответственно.

Построение Мультипликативной модели рассмотрим на данных предыдущего примера.

Шаг 1. Методика, применяемая на этом шаге, полностью совпадает с методикой построения аддитивной модели.

Таблица 4.8

№ квартала, T	Объем Потребления Электроэнергии,	Итого За четыре Квартала	Скользящая Средняя За четыре Квартала	Центрированная Скользящая Средняя	Оценка Сезонной Компоненты
1	2	3	4	5	6
1	375	–	–	–	–
2	371	2630	657,5	–	–
3	869	2612	653	655,25	1,3262
4	1015	2712	678	665,5	1,5252
5	357	2835	708,75	693,75	0,5146
6	471	2840	710	709,375	0,6640
7	992	2873	718,25	714,125	1,3891
8	1020	2757	689,25	703,75	1,4494
9	390	2757	689,25	689,25	0,5658
10	355	2642	660,5	674,875	0,5260
11	992	2713	678,25	669,375	1,4820
12	905	2812	703	690,625	1,3104
13	461	2740	685	694	0,6643
14	454	2762	690,5	687,75	0,6601
15	920	–	–	–	–
16	927	–	–	–	–

Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 6 табл. 4.8). Эти оценки используются для расчета сезонной компоненты S (табл. 4.9). Для этого найдем средние за каждый квартал оценки сезонной компоненты . Так же как и в аддитивной модели считается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4.

Имеем

.

Определяем корректирующий коэффициент:

.

Скорректированные значения сезонной компоненты получаются при умножении ее средней оценки на корректирующий коэффициент K.

Проверяем условие равенство 4 суммы значений сезонной компоненты:

.

Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. В результате получим величины (гр. 4 табл. 4.10), которые содержат только тенденцию и случайную компоненту.

Таблица 4.10

T				T
1	2	3	4	5	6	7
1	375	0,5779	648,9012	654,9173	378,4767	0,9908
2	371	0,6128	605,4178	658,1982	403,3439	0,9198
3	869	1,3901	625,1349	661,4791	919,5221	0,9451
4	1015	1,4192	715,1917	664,7600	943,4274	1,0759
5	357	0,5779	617,7539	668,0409	386,0608	0,9247
6	471	0,6128	768,6031	671,3218	411,3860	1,1449
7	992	1,3901	713,6177	674,6027	937,7652	1,0578
8	1020	1,4192	718,7148	677,8836	962,0524	1,0602
9	390	0,5779	674,8572	681,1645	393,6450	0,9907
10	355	0,6128	579,3081	684,4454	419,4281	0,8464
11	992	1,3901	713,6177	687,7263	956,0083	1,0377
12	905	1,4192	637,6832	691,0072	980,6774	0,9228
13	461	0,5779	797,7159	694,2881	401,2291	1,1490
14	454	0,6128	740,8616	697,5690	427,4703	1,0621
15	920	1,3901	661,8229	700,8499	974,2515	0,9443
16	927	1,4192	653,1849	704,1308	999,3024	0,9277

Шаг 4. Определим компоненту T в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни . В результате получим уравнение тренда:

.

Подставляя в это уравнение значения , найдем уровни T для каждого момента времени (гр. 5 табл. 4.10).

Шаг 5. Найдем уровни ряда, умножив значения T на соответствующие значения сезонной компоненты (гр. 6 табл. 4.10). На одном графике откладываем фактические значения уровней временного ряда и теоретические, полученные по мультипликативной модели.

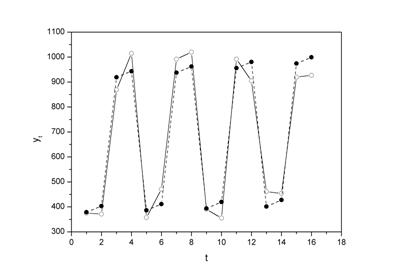
Рис. 4.7.

Расчет ошибки в мультипликативной модели производится по формуле:

.

Для сравнения мультипликативной модели и других моделей временного ряда можно, по аналогии с аддитивной моделью, использовать сумму квадратов абсолютных ошибок :

.

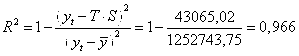Сравнивая показатели детерминации аддитивной и мультипликативной моделей, делаем вывод, что они примерно одинаково аппроксимируют исходные данные.

Шаг 6. Прогнозирование по мультипликативной модели. Если предположить, что по нашему примеру необходимо дать прогноз об общем объеме потребления электроэнергии на I и II кварталы 2003 года, прогнозное значение уровня временного ряда в мультипликативной модели есть произведение трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда

.

Получим

;

.

Значения сезонных компонент за соответствующие кварталы равны: и . Таким образом

;

.

Т. е. в первые два квартала 2003 г. следовало ожидать объема потребления электроэнергии порядка 409 и 436 кВт соответственно.

Таким образом, аддитивная и мультипликативная модели дают примерно одинаковый результат по прогнозу.

< Предыдущая		Следующая >