17. Автокорреляция уровней временного ряда

При наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Корреляционную зависимость между последовательными уровнями временного ряда называют Автокорреляцией уровней ряда.

Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени.

Формула для расчета коэффициента автокорреляции имеет вид:

(4.1)

Где

.

Эту величину называют Коэффициентом автокорреляции уровней ряда первого порядка, так как он измеряет зависимость между соседними уровнями ряда и .

Аналогично можно определить коэффициенты автокорреляции второго и более высоких порядков. Так, коэффициент автокорреляции второго порядка характеризует тесноту связи между уровнями и и определяется по формуле:

(4.2)

Где

Число периодов, по которым рассчитывается коэффициент автокорреляции, называют Лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Считается целесообразным для обеспечения статистической достоверности коэффициентов автокорреляции использовать правило – максимальный лаг должен быть не больше .

Свойства коэффициента автокорреляции.

1. Он строится по аналогии с линейным коэффициентом корреляции и также характеризует тесноту только линейной связи текущего и предыдущего уровней ряда. Поэтому по коэффициенту автокорреляции можно судить о наличии линейной (или близкой к линейной) тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу второго порядка или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю.

2. По знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство временных рядов экономических данных содержат положительную автокорреляцию уровней, однако при этом могут иметь убывающую тенденцию.

Последовательность коэффициентов автокорреляции уровней первого, второго и т. д. порядков называют Автокорреляционной функцией временного ряда. График зависимости ее значений от величины лага (порядка коэффициента автокорреляции) называется Коррелограммой.

Анализ автокорреляционной функции и коррелограммы позволяет определить лаг, при котором автокорреляция наиболее высокая, а, следовательно, и лаг, при котором связь между текущим и предыдущими уровнями ряда наиболее тесная, т. е. при помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.

Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка , то ряд содержит циклические колебания с периодичностью в моментов времени. Если ни один из коэффициентов автокорреляции не является значимым, можно сделать одно из двух предположений относительно структуры этого ряда: либо ряд не содержит тенденции и циклических колебаний, либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ. Поэтому коэффициент автокорреляции уровней и автокорреляционную функцию целесообразно использовать для выявления во временном ряде наличия или отсутствия трендовой компоненты и циклической (сезонной) компоненты.

Рассмотрим Пример. Пусть имеются некоторые условные данные об общем объеме потребления электроэнергии на одном из предприятий города.

Таблица 4.1

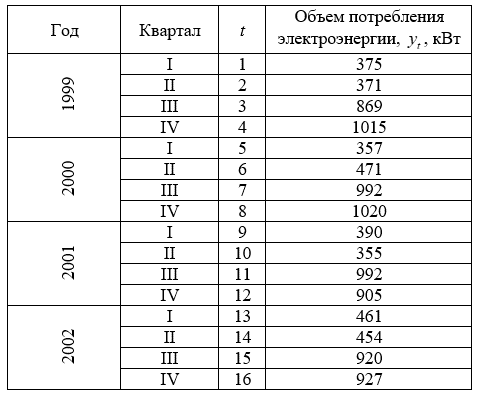
Построим поле корреляции:

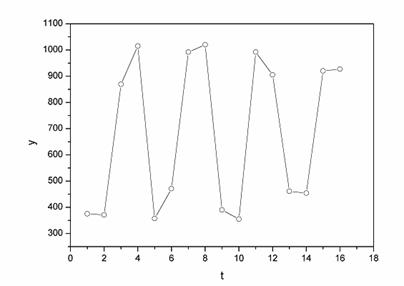
Рис. 4.4.

Уже исходя из графика видно, что значения Y образуют пилообразную фигуру.

Рассчитаем несколько последовательных коэффициентов автокорреляции. Для этого составляем первую вспомогательную таблицу (см. табл. 4.2).

Следует заметить, что среднее значение получается путем деления не на 16, а на 15, т. к. у нас теперь на одно наблюдение меньше.

Теперь вычисляем коэффициент автокорреляции первого порядка по формуле (4.1):

.

Составляем вспомогательную таблицу 4.3 для расчета коэффициента автокорреляции второго порядка.

Следовательно

.

Аналогично находим коэффициенты автокорреляции более высоких порядков, а все полученные значения заносим в сводную таблицу 4.4.

Таблица 4.2

T
1	2	3	4	5	6	7	8
1	375	–	–	–	–	–	–
2	371	375	–328,33	–288,13	94601,72	107800,59	83018,90
3	869	371	169,67	–292,13	–49565,70	28787,91	85339,94
4	1015	869	315,67	205,87	64986,98	99647,55	42382,46
5	357	1015	–342,33	351,87	–120455,66	117189,83	123812,50
6	471	357	–228,33	–306,13	69898,66	52134,59	93715,58
7	992	471	292,67	–192,13	–56230,69	85655,73	36913,94
8	1020	992	320,67	328,87	105458,74	102829,25	108155,48
9	390	1020	–309,33	356,87	–110390,60	95685,05	127356,20
10	355	390	–344,33	–273,13	94046,85	118563,15	74600,00
11	992	355	292,67	–308,13	–90180,41	85655,73	94944,10
12	905	992	205,67	328,87	67638,69	42300,15	108155,48
13	461	905	–238,33	241,87	–57644,88	56801,19	58501,10
14	454	461	–245,33	–202,13	49588,55	60186,81	40856,54
15	920	454	220,67	–209,13	–46148,72	48695,25	43735,36
16	927	920	227,67	256,87	58481,59	51833,63	65982,20
Сумма	10499	9947	9,05	0,05	74085,16	1153766,39	1187469,73
Среднее Значение	699,933	663,133	–	–	–	–	–

Таблица 4.3

T
1	2	3	4	5	6	7	8
1	375	–	–	–	–	–	–
2	371	–	–	–	–	–	–
3	869	375	145,57	–269,79	‑39273,33	21190,62	72786,64
4	1015	371	291,57	–273,79	‑79828,95	85013,06	74960,96
5	357	869	–366,43	224,21	‑82157,27	134270,94	50270,12
6	471	1015	–252,43	370,21	‑93452,11	63720,90	137055,44
7	992	357	268,57	–287,79	‑77291,76	72129,84	82823,08
8	1020	471	296,57	–173,79	‑51540,90	87953,76	30202,96
9	390	992	–333,43	347,21	‑115770,23	111175,56	120554,78
10	355	1020	–368,43	375,21	‑138238,62	135740,66	140782,54
11	992	390	268,57	–254,79	‑68428,95	72129,84	64917,94
12	905	355	181,57	‑289,79	‑52617,17	32967,66	83978,24
13	461	992	–262,43	347,21	‑91118,32	68869,50	120554,78
14	454	905	–269,43	260,21	‑70108,38	72592,52	67709,24
15	920	461	196,57	‑183,79	‑36127,60	38639,76	33778,76
16	927	454	203,57	‑190,79	‑38839,12	41440,74	36400,82
Сумма	10128	9027	–0,02	‑0,06	‑1034792,71	1037835,43	1116776,36
Среднее Значение	723,43	644,79	–	–	–	–	–

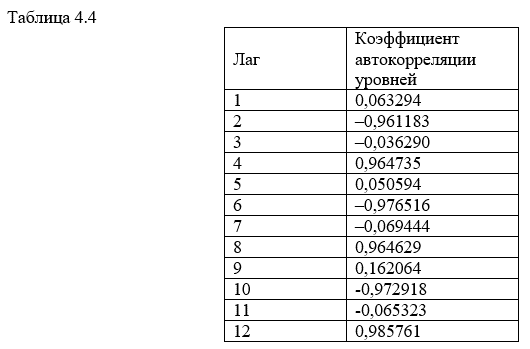
Коррелограмма:

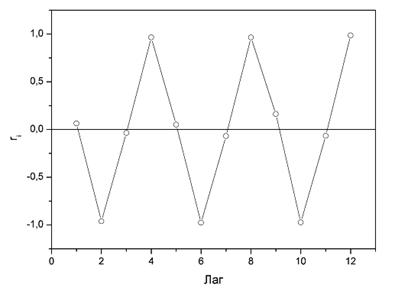
Рис. 4.5.

Анализ коррелограммы и графика исходных уровней временного ряда позволяет сделать вывод о наличии в изучаемом временном ряде сезонных колебаний периодичностью в четыре квартала.

< Предыдущая		Следующая >