09. Отбор факторов для построения модели

На этом этапе анализируются связи между факторами (наличие коллинеарных зависимостей), а также связи каждого фактора с у. Подобный анализ называется корреляционным анализом, использующим показатели тесноты связи (ТС).

Для интерпретации ТС приведем следующие схемы (поля корреляции).

Полем корреляции или Диаграммой рассеяния называют совокупность значений пар показателей (у и xi или xi и xj) в двумерной системе координат.

На рис. (а) разброс точек незначительный, вариация исследуемого показателя Y очень сильно связана с вариацией фактора . На рис. (б) связь между Y и незначительна. Если фактор тесно связан с исследуемым показателем, т. е. вариация фактора связана с вариацией Y, то изменяя в нужном направлении величину фактора можно управлять исследуемым показателем.

Различают Парные И Многофакторные связи. Соответственно существуют Парные и многофакторные показатели ТС.

В зависимости от вида связи - Линейная и Нелинейная - различают показатели ТС, характеризующие связь при линейной форме (Коэффициент корреляции) и показатели ТС, способные выражать ТС при любой форме связи (Корреляционное отношение, индекс корреляции).

Парный коэффициент корреляции служит мерой линейной взаимосвязи между двумя измеренными величинами. Он может принимать значения от -1 до +1. Если он равен нулю, то линейная связь между y и или между и отсутствует. Если он равен +1 или -1, то связь строго линейная. Отрицательный знак у коэффициента корреляции свидетельствует об обратной связи y и или и , а положительный - о прямой линейной зависимости.

Считается, что коэффициент корреляции равный нулю показывает отсутствие связи, но это не всегда верно. Исключение из этого правила, возможно, по нескольким причинам:

1. Следует различать связи формальные и причинно-следственные. Если КК большой, то это не значит, что существует причинная связь между рассматриваемыми показателями.

2. Нулевое значение парного КК также не означает отсутствие связи т. к. в случае нелинейной зависимости коэффициент парной корреляции тоже равен нулю.

Коэффициент парной корреляции позволяет выявить структуру связи для изучаемого объекта. Это свойство оказывается полезным для планирования мероприятия по процессам управления объектом.

Парный коэффициент корреляции можно вычислить по формулам 1.9 или 1.10.

Взаимосвязь между факторами наглядно можно представить в виде матрицы коэффициентов корреляции:

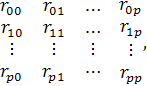(1.27)

Где 0 – индекс исследуемого показателя;

1, 2, …, p – индексы соответствующих факторов.

Коэффициенты парной корреляции позволяют провести анализ коллинеарности и мультиколлинеарности факторов. Коллинеарными называются такие факторы, теснота связи между которыми очень высока (значение парного коэффициента для таких факторов >=0,8). Если тесно связанных факторов несколько, то такие факторы называются Мультиколлинеарными. С экономической точки зрения тесно связанные факторы могут описывать одни и те же условия формирования исследуемого показателя. В регрессионную модель не должны включаться такие факторы, характеризующие одни и те же причины (условия).

Для решения вопроса о том, какой (какие) из факторов следует исключить из дальнейшего анализа, рекомендуется поступать следующим образом: если имеются факторы, теснота связи между которыми , то нужно сравнить соответствующие значения коэффициентов и . Если , то -ый фактор следует оставить в модели, а J-ый исключить.

Множественный коэффициент корреляции R является мерой линейной зависимости между И набором факторов. Границы изменения R от 0 до 1. Нулевое значение этого коэффициента указывает, что не зависит (линейно) от набора факторов, а значение 1 указывает на полную линейную зависимость. Расчет коэффициента множественной корреляции производится по формуле:

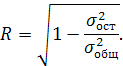(1.28)

На основе множественного коэффициента корреляции можно вычислить Множественный коэффициент детерминации

- показывает, на сколько % факторы, включенные в модель детерминируют, т. е. оказывают влияние на результирующий показатель. Также по нему оценивают полноту модели.

Частные коэффициенты корреляции рассчитываются для определения доли вариаций показателей, вызываемые некоторым фактором или группой факторов. Показатель позволяет получить уточненные оценки влияния факторов на результирующий показатель.

Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии. Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель. Чистое влияние фактора х2 на результат у можно найти по формуле:

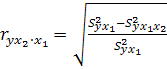. (1.29)

Аналогично определяется и чистое влияние на результат у фактора х1:

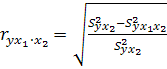. (1.30)

Справедлива также следующая формула, связывающая коэффициенты частной и обычной корреляции:

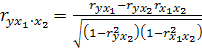. (1.31)

Значения частного коэффициента корреляции лежат в интервале [-1,1], как у обычного коэффициента корреляции. Если , это означает отсутствие прямого (линейного) влияния переменной х1 и у.

Корреляционное отношение является универсальным показателем ТС, характеризующим ТС при любом виде связи (линейная или нелинейная) между и , рассчитывается таким образом

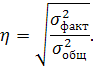(1.32)

Границы изменения корреляционного отношения такие же: от 0 до 1.

Для парной зависимости при линейной связи выполняется соотношение Если η и r различаются больше, чем на 5 %, то нелинейность считается существенной, а для построенной модели необходимо использовать нелинейную зависимость.

В связи с тем, что показатели ТС рассчитываются по ограниченному числу наблюдений, необходима их проверка на надежность. При этой проверке устанавливается, существенно ли отличается показатель ТС от нуля. Для проверки этой гипотезы используют t-критерий (критерий Стьюдента). Вычисляется расчетное значение этого коэффициента:

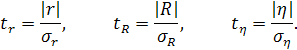(1.33)

Среднеквадратические ошибки вычисляются соответственно

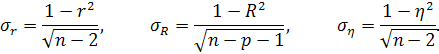(1.34)

Расчетное значение t-критерия сравнивается с табличным. Если t-расчетное > t - табличного, то проверяемый показатель считается надежным. Табличное значение t-критерия определяется при уровне значимости и числе степеней свободы K. Уровень значимости, как правило, принимается равным 0,05 или 0,01. При таком α можно с доверительной вероятностью соответственно 0,95 или 0,99 утверждать, статистически значим или нет соответствующий показатель ТС.

Число степеней свободы k равно:

Для R

для R

для H

< Предыдущая		Следующая >