1.10. Нелинейная связь между переменными
Разумеется, связь между конкретными экономическими факторами вовсе не обязана быть линейной.
Например, если мы рассматриваем зависимость от располагаемого дохода ![]() Не всех Затрат на личное потребление, а лишь затрат
Не всех Затрат на личное потребление, а лишь затрат ![]() на некоторый Продукт питания (или группу продуктов питания), например, на куриные яйца, то уже по чисто физиологическим причинам функция связи
на некоторый Продукт питания (или группу продуктов питания), например, на куриные яйца, то уже по чисто физиологическим причинам функция связи
![]()
Скорее всего, должна Замедлять свой рост при возрастании ![]() , Так что возможный график этой функции имеет вид
, Так что возможный график этой функции имеет вид

В такой ситуации нельзя говорить о склонности к потреблению данного продукта как о постоянной величине. Вместо этого, в рассмотрение вводят понятие Предельной (Marginal) Склонности к потреблению (MPC), которая для заданной величины ![]() Располагаемого дохода определяется формулой
Располагаемого дохода определяется формулой
![]()
Иначе говоря,
![]()
Замедление скорости роста функции ![]() соответствует Убыванию
соответствует Убыванию ![]() С возрастанием
С возрастанием ![]() . Уточняя предположения о поведении
. Уточняя предположения о поведении ![]() , Можно получить ту или иную форму связи между переменными
, Можно получить ту или иную форму связи между переменными ![]() и
и ![]() .
.
Среди прочих возможных форм связи между ![]() и
и ![]() отметим Степенную связь
отметим Степенную связь
![]()
В которой ![]() . Для такой связи
. Для такой связи
![]()
Так что предельная склонность к потреблению Монотонно убывает с ростом ![]() .
.
Степенную форму связи можно привести к линейной форме, если вместо уровней дохода и расходов на потребление рассмотреть Логарифмы уровней по какому-нибудь (но одному и тому же!) основанию (например, натуральные или десятичные логарифмы).
Действительно, переходя к логарифмам уровней, получаем соотношение
![]()
Или, обозначая ![]()
![]()
Линейной модели связи в логарифмах соответствует линейная модель наблюдений
![]()
Которую мы уже умеем оценивать.
Заметим, что коэффициент ![]() в последних выражениях есть не что иное как
в последних выражениях есть не что иное как
![]()
Эта величина не зависит от выбора основания логарифмов, так что
![]()
Где используются Натуральные логарифмы.
Вообще, если мы имеем связь между какими-то переменными экономическими факторами ![]() И
И ![]() в виде
в виде
![]()
То мы определяем функцию
![]()
Как Предельную склонность Y по отношению к X.
В экономической теории существенную роль играет Функция эластичности, определяемая как предел
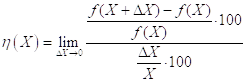
Отношения Процентного изменения ![]() к Процентному изменению
к Процентному изменению ![]() , когда последнее Стремится к нулю. Правую часть последнего соотношения можно записать в виде
, когда последнее Стремится к нулю. Правую часть последнего соотношения можно записать в виде
![]()
Заметим также, что
![]()
Так что
![]()
Значение ![]() равно угловому коэффициенту касательной к графику функции
равно угловому коэффициенту касательной к графику функции ![]() при
при ![]() , тогда как значение
, тогда как значение ![]() равно угловому коэффициенту касательной к графику зависимости
равно угловому коэффициенту касательной к графику зависимости ![]() от
от ![]() при
при ![]() . Как следствие, условие постоянства
. Как следствие, условие постоянства ![]() , т. е.
, т. е. ![]() , Означает Линейную связь между уровнями факторов
, Означает Линейную связь между уровнями факторов
![]()
А условие постоянства эластичности ![]() означает Линейную связь между логарифмами уровней
означает Линейную связь между логарифмами уровней
![]()
Соответствующую степенной связи между уровнями
![]()
Выражающей степенное возрастание (при ![]() ) или убывание (при
) или убывание (при ![]() ) уровней фактора
) уровней фактора ![]() при возрастании уровней фактора
при возрастании уровней фактора ![]() .
.
Заметим, что если ![]() , то эту постоянную можно трактовать как Процентное изменение уровня фактора
, то эту постоянную можно трактовать как Процентное изменение уровня фактора ![]() При изменении фактора
При изменении фактора ![]() На 1%.
На 1%.
Отметим также, что в модели ![]() функция эластичности имеет вид
функция эластичности имеет вид

И при ![]() возрастает от
возрастает от ![]() до
до ![]() с возрастанием значений
с возрастанием значений ![]() От
От ![]() до
до ![]() . Если
. Если ![]() , то
, то ![]() . При
. При ![]() функция эластичности
функция эластичности ![]() убывает от
убывает от ![]() до
до ![]() , когда
, когда ![]() изменяется от
изменяется от ![]() до
до ![]() .
.
К линейной форме связи можно привести и некоторые другие виды зависимости, характерные для экономических моделей.
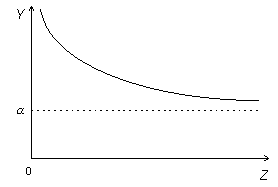
Так, если ![]() — объем плановых инвестиций, а
— объем плановых инвестиций, а ![]() — Норма процента, то между ними существует связь, которая иногда может быть выражена в форме
— Норма процента, то между ними существует связь, которая иногда может быть выражена в форме
![]()
И имет графическое представление
Заменой переменной ![]() приводим указанную связь к линейной форме
приводим указанную связь к линейной форме ![]() В этой модели эластичность
В этой модели эластичность ![]() По
По ![]() отрицательна и Меньше единицы по абсолютной величине:
отрицательна и Меньше единицы по абсолютной величине:
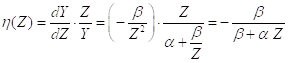
![]()
(«объем плановых инвестиций Неэластичен по отношению к норме процента»).
В моделях «доход — потребление», относящихся к потреблению Продуктов питания, линейная модель в логарифмах уровней, выражающая уменьшение ![]() С возрастанием
С возрастанием ![]() , Все же Не всегда удовлетворительна, поскольку Эластичность в такой модели постоянна. Опять же по чисто физиологическим причинам, скорее более подходящей будет модель связи с Убывающей (в конечном счете) Эластичностью. Такого рода связь между факторами
, Все же Не всегда удовлетворительна, поскольку Эластичность в такой модели постоянна. Опять же по чисто физиологическим причинам, скорее более подходящей будет модель связи с Убывающей (в конечном счете) Эластичностью. Такого рода связь между факторами ![]() и
и ![]() может иметь вид
может иметь вид
![]()
(См. следующий график, построенный при A = 5, B = 10.)
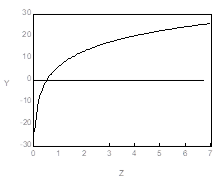
Действительно,
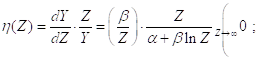
Однако, здесь возникают проблемы с Отрицательными значениями ![]() при малых значениях
при малых значениях ![]() .
.
Последнего недостатка нет в модели
![]()
Т. е.
![]()
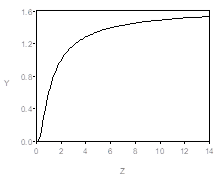
(График построен при значениях A =0.1, B =1.) Здесь
![]()
(закон Энгеля убывания эластичности потребления продуктов питания по доходу).
Обе последние модели сводятся к линейной форме связи путем перехода от уровней переменных к их логарифмам или обратным величинам.
Замечание
Если исследователь принимает модель наблюдений
![]()
То тем самым, он соглашается тем, что
![]()
Или
![]()
Т. е. соглашается с мультипликативным вхождением ошибок ![]() В нелинейное уравнение для
В нелинейное уравнение для ![]() .
.
В то же время, не исключено, что по существу дела модель должна иметь вид
![]()
Т. е. имеет Аддитивные ошибки. В последнем случае взятие логарифмов от обеих частей Не приводит к линейной модели наблюдений. В такой ситуации оценки наименьших квадратов параметров ![]() и
и ![]() приходится получать Итерационными методами, в процессе реализации которых производится Последовательное приближение к минимуму суммы квадратов
приходится получать Итерационными методами, в процессе реализации которых производится Последовательное приближение к минимуму суммы квадратов
![]()
| < Предыдущая | Следующая > |
|---|