2.2.5. Производные основных элементарных функций

Используя полученные формулы и свойства производных, найдем производные основных элементарных функций.

1. Если f(x)=C=const, то ΔС=0, поэтому С΄=0.

2. у=xn, где n – натуральное число. Тогда по формуле бинома Ньютона можно представить

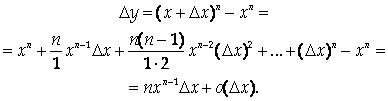
Следовательно, у΄ = nxn-1.

3. y = sin x,

4. y = cos x,

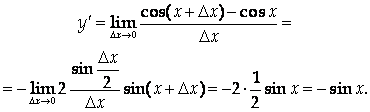
5. y = tg x,

6. Аналогично можно получить формулу

(см. 2-е следствие из второго замечательного предела).

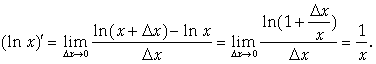
(см. 1-е следствие из второго замечательного предела).

Таким же образом можно найти производные остальных гиперболических функций.

10. По формуле производной обратной функции

11. Если a – произвольное действительное число, то

В результате получена таблица основных производных:

< Предыдущая		Следующая >