1.4.2. Точки разрыва и их классификация
Пусть функция f(x) определена в некоторой окрестности точки х0, за исключением, возможно, самой этой точки. Тогда х0 называется точкой разрыва функции f(x), если она либо не определена при х = х0, либо не является непрерывной в точке х0.
|
Если существует конечный предел f(x) при х→х0, но не равный f(x0), точка разрыва х0 называется устранимой особенностью. |
Термин «устранимая особенность» связан с тем, что, доопределив функцию в точке разрыва значением ее предела в этой точке, мы сделаем ее непрерывной при х = х0, то есть устраним разрыв в рассматриваемой точке.
|
Если существуют конечные односторонние пределы f(x) при |
|
Все остальные точки разрыва называются точками разрыва 2-го рода. |
Примеры.
![]()
![]()
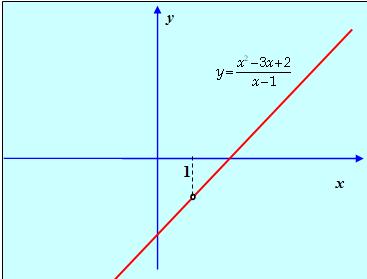
Функция не определена при х = 1, а для остальных значений аргумента может быть представлена как у = х - 2. Следовательно,
![]()
То есть х = 1 – устранимая особенность.
![]()
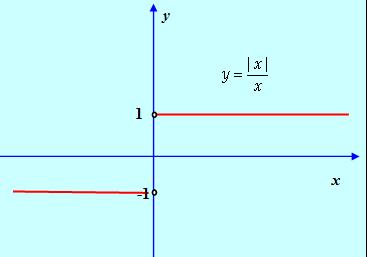
Из определения модуля следует, что у = 1 при x > 0, y = -1 при x < 0, а при х = 0 функция не определена. При этом
![]()
Следовательно, х = 0 –точка разрыва 1-го рода.
![]()
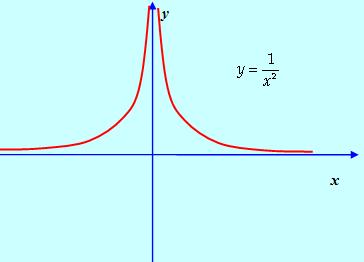
Функция не определена при х = 0 , и
![]()
Поэтому х = 0 – точка разрыва 2-го рода.
![]()
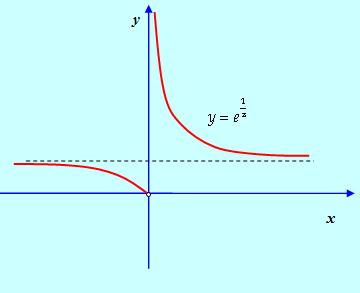
![]()
То есть правосторонний предел не является конечным. Значит, х = 0 – точка разрыва 2-го рода.
![]()

Функция не определена при х = 0 и не имеет предела при х→0. Следовательно, х = 0 – точка разрыва 2-го рода.
| < Предыдущая | Следующая > |
|---|