1.2.8. Примеры решения задач по теме «Свойства пределов. Замечательные пределы»

Задача 1.

Вычислить предел

Указание

Преобразуйте числитель, воспользовавшись формулой

А затем разделите обе части дроби на Х2.

Решение

Преобразуем в числителе разность косинусов в произведение:

Теперь разделим обе части дроби на Х2 и используем 1-й замечательный предел:

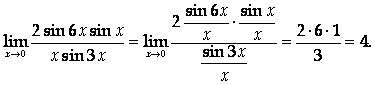
Ответ: 4.

Задача 2.

Вычислить предел

Указание

Сделайте замену переменной: T = P - X.

Решение

Сделаем замену переменной: T = P - X. Тогда, используя периодичность тригонометрических функций и формулы приведения, получим:

Подставим эти результаты в выражение, стоящее под знаком предела:

Ответ: -1.

Задача 3.

Вычислить предел

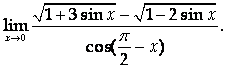
Указание

Домножьте числитель и знаменатель на выражение, сопряженное числителю (то есть на сумму соответствующих корней), а в знаменателе примените формулу приведения.

Решение

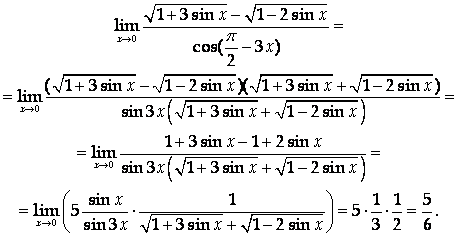
Ответ:

Задача 4.

Вычислить предел

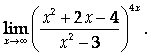
Указание

Преобразуйте функцию к виду

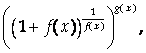
Где

Решение

Ответ: Е8.

Задача 5.

Вычислить предел

Указание

Воспользуйтесь следствием из 2-го замечательного предела:

Решение

Умножим обе части дроби на sin12X:

Ответ: 3.

Задача 6.

Вычислить предел

Указание

Воспользуйтесь следствием из 2-го замечательного предела:

Решение

Вынесем за скобки в числителе Ех и разделим обе части дроби на Х:

Ответ:

Задача 7.

Вычислить предел

Указание

Преобразуйте функцию к виду

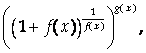
Где

Решение

Ответ:

Задача 8.

Вычислить предел

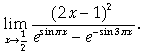
Указание

Сделайте замену переменной

И воспользуйтесь следствием из 2-го замечательного предела:

Решение

Сделаем замену переменной

Тогда

Подставляя в первоначальное выражение, получаем:

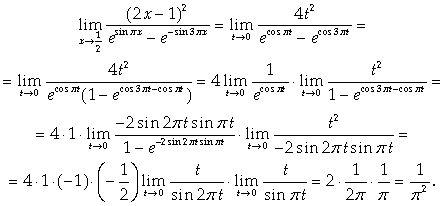
Ответ:

< Предыдущая		Следующая >