1.2.5. Второй замечательный предел (Теорема)

Замечание. Число е2,7.

Доказательство.

1. Докажем сначала, что последовательность

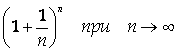
Имеет предел, заключенный между 2 и 3. По формуле бинома Ньютона

Возрастающая переменная величина при возрастающем n. С другой стороны,

И т. д., поэтому

Следовательно,

Ограниченная и возрастающая величина, поэтому она имеет предел (см. теорему 6). Значение этого предела обозначается числом е.

2. Докажем, что

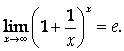
А) Пусть . Тогда

При Найдем пределы левой и правой частей неравенства:

Следовательно, по лемме о двух милиционерах

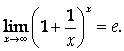
Б) Если и

Теорема доказана.

< Предыдущая		Следующая >