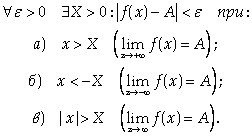1.1.4. Пределы функций
Определим понятие Окрестности точки Х0 как множество значений Х, являющихся решениями неравенства 0<|X - x0| < D, где D > 0 – некоторое число. Само значение Х0 может включаться в окрестность или не включаться в нее (в этом случае окрестность называется проколотой).
Пусть функция У = F(X) определена в некоторой окрестности точки Х0.
|
Число А называется Пределом функции у = F(X) при х, стремящемся к х0, если
Такое, что
|
Обозначение:
![]()
Замечание. Для существования предела функции в точке Х0 не требуется, чтобы функция была определена в самой этой точке.
Примеры.
1. Докажем, что
![]()
Если |2X+1-7| < E, то |2X - 6| < E, |X - 3| < E/2. Таким образом, если принять D(E) = E/2, то выполнены все условия определения предела. Утверждение доказано.
2. ![]()
Заметим, что в проколотой окрестности х=2 Х – 2 не равно нулю, поэтому мы имеем право сократить дробь на (Х - 2).
|
Функция у = F(X) имеет Бесконечный предел При х, стремящемуся к х0 (стремится к бесконечности, является бесконечно большой), если
|
Обозначение:
![]()
|
Число А называется Пределом функции Y = F(X) на бесконечности, если
|
Замечание. Бесконечный предел функции на бесконечности можно определить по аналогии с двумя предыдущими определениями.
Определение. Функция У = F(X) называется Ограниченной В некоторой области значений Х, если существует число М>0 такое, что |F(X)|<M для всех значений Х, принадлежащих рассматриваемой области.
| < Предыдущая | Следующая > |
|---|