11. Локальный экстремум функции нескольких переменных
1°. Точка ![]() Называется точкой локального максимума функции
Называется точкой локального максимума функции ![]() , если найдется такая e-окрестность т.
, если найдется такая e-окрестность т. ![]()
![]() , что для всех точек этой окрестности
, что для всех точек этой окрестности ![]() выполняется неравенство:
выполняется неравенство:
![]()
И точкой локального минимума, если
![]() .
.
Максимумы и минимумы функции называются ее экстремумами.
2°. Теорема (необходимый признак экстремума). Если функция ![]() дифференцируема в т.
дифференцируема в т. ![]() и имеет в этой точке экстремум, то все ее частные производные первого порядка в т.
и имеет в этой точке экстремум, то все ее частные производные первого порядка в т. ![]() равны нулю:
равны нулю:
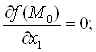
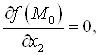 ...
... 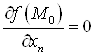 .
.
3°. Точки экстремума функции принадлежат множеству критических точек, которое состоит из стационарных (в которых все производные первого порядка равны нулю) и точек, в которых хотя бы одна из производных первого порядка не существует.
4°. Теорема (достаточный признак экстремума дважды дифференцируемой функции).
Пусть ![]() дважды дифференцируемая в т.
дважды дифференцируемая в т. ![]() и точка
и точка ![]() — ее стационарная точка. Если второй дифференциал функции
— ее стационарная точка. Если второй дифференциал функции ![]() представляет собой положительно определенную квадратичную форму относительно
представляет собой положительно определенную квадратичную форму относительно ![]() , то
, то ![]() — точка минимума, если
— точка минимума, если ![]() — отрицательно определенная форма, то
— отрицательно определенная форма, то ![]() — точка максимума,, если
— точка максимума,, если ![]() — знакопеременная квадратичная форма, то в т.
— знакопеременная квадратичная форма, то в т. ![]() экстремума нет.
экстремума нет.
5°. Пусть ![]() — функция двух переменных.
— функция двух переменных.
![]() — стационарная точка.
— стационарная точка.
Обозначим
![]() ;
;  ;
;  .
.
Тогда:
1) если  то в т.
то в т. ![]() — экстремум.
— экстремум.
Причем максимум, если ![]() и минимум, если
и минимум, если ![]() .
.
2) если ![]() то в т.
то в т. ![]() экстремума нет.
экстремума нет.
3) если D = 0, то т. ![]() может являться точкой экстремума, а может не являться экстремумом. В данном случае теорема ответа не дает.
может являться точкой экстремума, а может не являться экстремумом. В данном случае теорема ответа не дает.
Примеры
1. Исследовать на экстремум функцию ![]() .
.
А) Находим стационарные точки функции. Для этого следует найти первые производные и приравнять их к нулю:
 .
.
Решая систему уравнений, находим 2 стационарные точки: ![]() и
и ![]() ;
;
Б) Для того, чтобы решать вопрос о том, являются ли найденные стационарные точки точками экстремума, следует найти все вторые производные: ![]()
![]()
![]() и вычислить их значения в стационарных точках:
и вычислить их значения в стационарных точках:


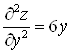 ,
,
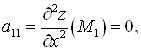
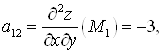
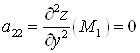 .
.
![]() в точке
в точке ![]() — экстремума нет.
— экстремума нет.
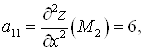
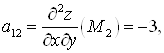
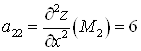 .
.
![]() в точке
в точке ![]() функция достигает экстремума и т. к.
функция достигает экстремума и т. к. ![]() то это минимум:
то это минимум: ![]()
2. Исследовать на экстремум функцию ![]() , заданную неявно:
, заданную неявно:
![]()
А) Для определения критических точек вычислим первые производные функции
 ,
,
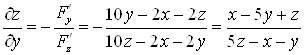 .
.
В точках, где ![]() , первые производные существуют, и стационарные точки определяются из системы уравнений:
, первые производные существуют, и стационарные точки определяются из системы уравнений:
 (1)
(1)
Обратите внимание: система относительно трех переменных состоит только из двух уравнений. К этой системе следует присоединить уравнение, задающее функцию ![]() :
:
![]() (2)
(2)
Из системы (1) легко выражаются ![]() и
и ![]() через
через ![]() :
: ![]()
![]()
Подставляя эти соотношения в (2), получаем:
![]() ,
,
![]() ;
; ![]() .
.
Таким образом, точки ![]() и
и ![]() — стационарные точки функции.
— стационарные точки функции.
Б) вычисляя вторые производные ![]()
![]()
![]() следует помнить, что переменная
следует помнить, что переменная ![]() является функцией
является функцией ![]() и
и ![]() .
.
 ,
,
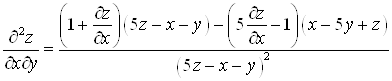 ,
,
 .
.
Заметьте, что подставлять в эти формулы ![]() и
и ![]() не нужно, поскольку производные второго порядка нужны только в стационарных точках, где
не нужно, поскольку производные второго порядка нужны только в стационарных точках, где ![]() и
и 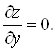
 ,
,
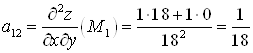 ,
,
 .
.

![]() — точка экстремума,
— точка экстремума, ![]()
![]() — точка
— точка ![]() .
. ![]()
В точке ![]()
 ;
;
![]() ;
; ![]() .
.
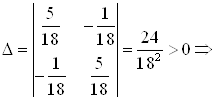
![]() — точка экстремума,
— точка экстремума, ![]()
![]() — точка минимума.
— точка минимума.
![]()
6°. Если ![]() — дважды дифференцируемая функция трех переменных и
— дважды дифференцируемая функция трех переменных и ![]() — стационарная точка, то для проверки достаточного признака экстремума следует вычислить все вторые производные функции в точке
— стационарная точка, то для проверки достаточного признака экстремума следует вычислить все вторые производные функции в точке ![]() :
:

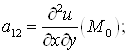
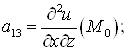
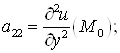
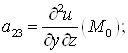

И составить матрицу ![]() Если все главные миноры матрицы D1, D2, D3 положительны, то в т.
Если все главные миноры матрицы D1, D2, D3 положительны, то в т. ![]() — минимум.
— минимум.
Если ![]() ,
, ![]() ,
, ![]() — в
— в ![]() — максимум.
— максимум.
Пример.
Исследователь на экстремум функцию
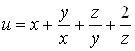 ,
, ![]() .
.
Решение:
А) Находим стационарные точки функции
![]() ;
; 
 ;
;


![]() . По условию задачи
. По условию задачи ![]() поэтому
поэтому ![]()
![]()
![]()
Б) ![]() ;
; ![]() ;
; ![]() ;
;
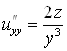 ;
;  ;
;
![]() ;
;
 ;
;
![]() ;
;
![]() ;
;
 ;
;
Точка ![]() — точка минимума.
— точка минимума.
![]() .
.
| < Предыдущая | Следующая > |
|---|