4. Признаки существования пределов

1. Теорема Больцано – Вейерштрасса.

Монотонная ограниченная последовательность имеет предел.

2. Теорема о «зажатой» последовательности.

Если и , то и .

3. Критерий Коши.

Для того чтобы последовательность имела конечный предел, необходимо и достаточно, чтобы для любого можно было указать такой номер , что для всех при любых .

Пример 13. Доказать, что последовательность с общим членом сходится:

.

Доказательство. Докажем, что эта последовательность монотонна и ограничена.

A) Так как , то , т. е. последовательность монотонно возрастает.

B) Так как при любом , то

;

Т. е. ; ограничена сверху.

Следовательно, предел последовательности существует.

Пример 14. Доказать, что последовательность сходится.

Доказательство.

A) Имеем , откуда ; т. е. последовательность монотонно убывает.

B) Так как при всех , то она ограничена снизу, значит, предел последовательности существует.

Пример 15. Найти пределы последовательностей с общими членами:

.

Решение. Находим:

,

.

Далее,

.

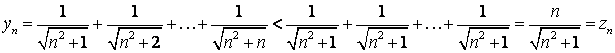С другой стороны,

.

Таким образом,

.

Следовательно, по теореме о «зажатой» последовательности

.

Пример 16. Пользуясь критерием Коши, доказать сходимость последовательности с общим членом

.

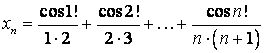Доказательство. Для произвольного и при всех натуральных имеем:

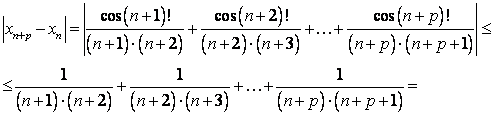
При и при всех натуральных .

Пример 17. Пользуясь критерием Коши, доказать расходимость последовательности с общим членом

.

Доказательство. Пусть – произвольное число из интервала .

Поскольку

,

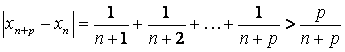А при

Для всех , то последовательность расходится.

< Предыдущая