7.7. Суть метода наименьших квадратов
Дальнейшие рассуждения будем проводить в предположении, что все измерения значений функции Y0, y1, y2,…, yN произведены с одинаковой точностью. Тогда оценка параметров А0, а1, а2,…, аn определяется из условия минимума суммы квадратов отклонений измеренных значений Yk от расчетных F(Xk; а0, а1, а2,…, аn):
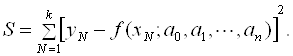(7.14)
Отыскание же значений параметров А0, а1, а2,…, аN, которые доставляют Min значение функции
(7.15)
Сводится к решению системы уравнений
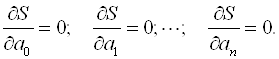(7.16)
Наиболее распространен способ выбора функции F(Xk; а0, а1, а2,…, аn) в виде линейной комбинации:
(7.17)
Здесь 
Базисные функции (известные); N << K; А0, а1, а2,…, аN – коэффициенты, определяемые методом наименьших квадратов. Запишем в явном виде условие (7.16), учитывая выражение (7.17):
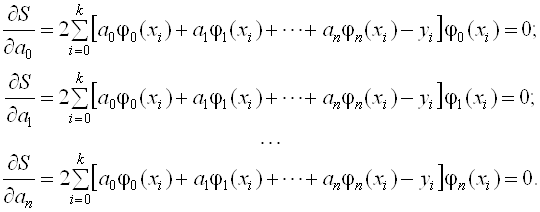(7.18)
Из системы линейных уравнений (7.18) определяются все коэффициенты Ak. Система (7.18) называется системой нормальных уравнений, матрица которой имеет вид
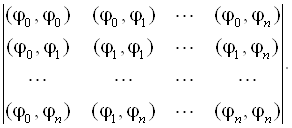(7.19)
Здесь
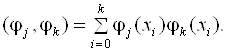(7.20)
Матрица (7.19) называется матрицей Грама. Расширенную матрицу получим добавлением справа столбца свободных членов:
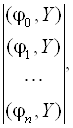(7.21),
Где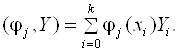 
(7.22)
Основные свойства матрицы Грама
1. Матрица симметрична относительно главной диагонали, то есть
.
2. Матрица является положительно определенной. Следовательно, при решении методом Гаусса можно воспользоваться схемой единственного деления.
3. Определитель матрицы будет отличен от нуля, если в качестве базиса выбраны линейно независимые функции 
; в этом случае система (7.18) имеет единственное решение.
В качестве базисных можно выбрать линейно независимые степенные функции
(7.23)
Следует учесть, что N << K. Тогда для этих функций расширенная матрица Грама примет вид
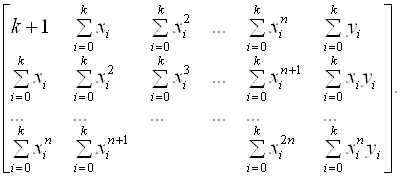(7.24)
Если выбрать N = K, то на основании единственности интерполяционного полинома получим функцию 
, совпадающую с каноническим интерполяционным полиномом степени K. При этом аппроксимирующая кривая пройдет через все экспериментальные точки, и функция S будет равна нулю.
Пример 7.2. Исходная функция Y = F(X) Задана в виде табл. 7.2:
Таблица 7.2
|
X |
10 |
15 |
17 |
20 |
|
Y |
3 |
7 |
11 |
17 |
Аппроксимируем экспериментальные данные линейной либо квадратичной функцией. Методом наименьших квадратов необходимо уточнить коэффициенты аппроксимирующего полинома.
1. При линейной аппроксимации исходную зависимость представим в виде 
, где 
. Методом наименьших квадратов определим A0 И A1. Расширенная матрица Грама в нашем случае имеет вид
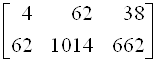Þ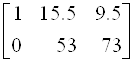 
; А1 = 1.3774; А0 =-11.8491.
Таким образом, аппроксимирующая функция равна
Оценим погрешность формулы, и результаты этой оценки сведем в табл. 7.3:
Таблица 7.3
|
X |
Y |
F |
Y - f |
|Y-f| / |y| |
|
10 |
3 |
1.9249 |
1.0751 |
0.3584 |
|
15 |
7 |
8.8119 |
-1.8119 |
0.2588 |
|
17 |
11 |
11.5667 |
-0.5667 |
0.0515 |
|
20 |
17 |
15.6989 |
1.3011 |
0.07654 |
Для нашей линейной функции S1 = 6.4528.
2. Решим ту же задачу, аппроксимировав эмпирические данные полиномом второй степени: 
.
Матрица Грама в этом случае имеет вид
Все результаты сведены в табл. 7.4.
Таблица 7.4
|
X |
Y |
F |
Y - f |
|Y-f| / |y| |
|
10 |
3 |
2.9511 |
0.0489 |
0.0163 |
|
15 |
7 |
7.3381 |
-0.3381 |
0.0483 |
|
17 |
11 |
10.6007 |
0.3993 |
0.0363 |
|
20 |
17 |
17.1101 |
-0.1101 |
0.0065 |
S2 = 0.2883.
Обсуждение результатов
1. Аппроксимировав эмпирические результаты более простой функцией (линейной), мы получили погрешность в различных узловых точках, лежащую в пределах от 5 до 35 %.
2. Более сложная формула квадратичной интерполяции обеспечивает погрешность не более 5 %.
3. Косвенную оценку погрешности можно провести, сравнив значения S1 И S2.
4. Матрица Грама для полинома второй, третьей степени имеет простой вид и может быть решена, например, методом Гаусса.
Вопросы для самопроверки
· В чем заключается задача интерполирования и аппроксимации?
· Запишите интерполяционные формулы Лагранжа и Ньютона.
· Какие требования предъявляются а) к интерполяционным полиномам;
б) к аппроксимационным полиномам?
· Что такое разделенные разности?
· В каких случаях применяются формулы Ньютона для интерполирования
а) вперед, б) назад?
· Что можно сказать о сходимости интерполяционных полиномов?
· Что такое обратное интерполирование, при каких условиях оно возможно (корректно)?
· В чем заключается идея метода наименьших квадратов?
· Что такое матрица Грама, каковы ее свойства?
· Что такое базисные функции? Можно ли в качестве базисных функций выбрать а) линейно независимые функции; б) линейно зависимые функции?
| < Предыдущая | Следующая > |
|---|
