7.5. Задача обратного интерполирования
Пусть функция Y = F(X) задана таблично. Задача обратного интерполирования заключается в том, чтобы по заданному значению функции Y определить соответствующее значение аргумента X.
Для случая неравноотстоящих значений аргумента X0, x1,…, xn задача может быть непосредственно решена с помощью интерполяционного многочлена Лагранжа. В этом случае достаточно принять переменную Y за независимую и написать формулу (аналог выражения (7.3)), выражающую Х как функцию У:
Можно также, считая У аргументом, использовать формулу Ньютона:
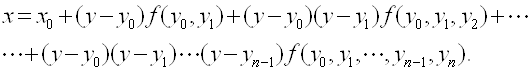 (7.11)
(7.11)
Замечание. Обратное интерполирование корректно только для взаимно однозначных функций.
Пример 7.1. Исходная функция Y = F(X) Задана табл. 7.1:
Таблица 7.1
|
X |
10 |
15 |
17 |
20 |
|
Y |
3 |
7 |
11 |
17 |
Необходимо найти значение функции Y при X = 12; найти значение X, для которого Y = 10.
Решение. В качестве примера задачу прямого интерполирования в начале таблицы с неравноотстоящими узлами решим по формулам Ньютона (7.8); для обратного интерполирования применим формулу Лагранжа (7.10).
Y(12) = f(X0) + (X –x0)F(X0, x1) + (X –x0) (X –x1) f(X0, x1, x2) +
+ (X –x0) (X –x1) (X –x2) f(X0, x1, x2, x3) = 3 + 2·0.8 +
+ 2·(-3)·0.02857 + 2·(-3)·(-5)·(-0.002857) = 4.3429.
X(10) = 10·3·(-1)·(-7)/[(-4)(-8)(-14)] + 15·7·(-1)·(-7)/[4·(-4)(-10)] +
+ 17·7·3(-7)/[8·4·(-6)] + 20·7·4·1/[14·10·6] = 16.641.
| < Предыдущая | Следующая > |
|---|
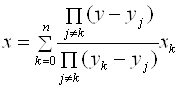 . (7.10)
. (7.10)