7.3. Интерполяционная формула Ньютона
Интерполяционная формула Ньютона позволяет выразить интерполяционный многочлен Pn(X) через значение F(X) в одном из узлов и через разделенные разности функции F(X), построенные по узлам X0, x1,…, xn. Эта формула является разностным аналогом формулы Тейлора:
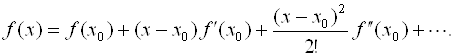 (7.4)
(7.4)
Прежде чем приводить формулу Ньютона, рассмотрим сведения о разделенных разностях. Пусть в узлах ![]() известны значения функции F(X). Предполагаем, что среди точек Xk, K = 0, 1,…, N нет совпадающих. Тогда разделенными разностями первого порядка называются отношения
известны значения функции F(X). Предполагаем, что среди точек Xk, K = 0, 1,…, N нет совпадающих. Тогда разделенными разностями первого порядка называются отношения
 (7.5)
(7.5)
Будем рассматривать разделенные разности, составленные по соседним узлам, то есть выражения ![]() . По этим разделенным разностям первого порядка можно построить разделенные разности второго порядка:
. По этим разделенным разностям первого порядка можно построить разделенные разности второго порядка:
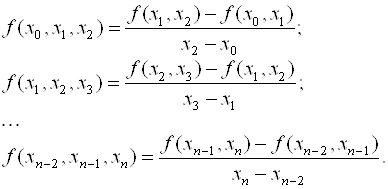 (7.6)
(7.6)
Аналогично определяются разности более высокого порядка. То есть пусть известны разделенные разности K-го порядка ![]() тогда разделенная разность K+1-го порядка определяется как
тогда разделенная разность K+1-го порядка определяется как
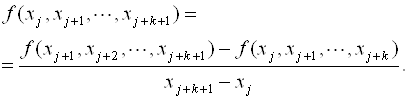 (7.7)
(7.7)
Интерполяционным многочленом Ньютона называется многочлен
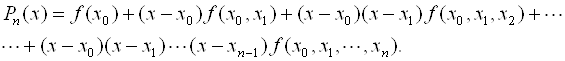 (7.8)
(7.8)
Показано, что интерполяционный многочлен Лагранжа (7.3) совпадает с интерполяционным многочленом Ньютона (7.8).
Замечания
· В формуле (7.8) не предполагалось, что узлы X0, X1,…, Xn расположены в каком-то определенном порядке. Поэтому роль точки X0 в формуле (7.8) может играть любая из точек X0, x1,…, xn. Соответствующее множество интерполяционных формул можно получить из (7.8), перенумеровав узлы. Например, тот же самый многочлен Pn(X) можно представить в виде
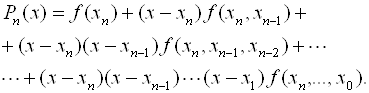 (7.9)
(7.9)
· Если ![]() то (7.8) называется формулой интерполирования вперед, а (7.9) - формулой интерполирования назад.
то (7.8) называется формулой интерполирования вперед, а (7.9) - формулой интерполирования назад.
· Интерполяционную формулу Ньютона удобнее применять в том случае, когда интерполируется одна и та же функция F(X), но число узлов интерполяции постепенно увеличивается. Если узлы интерполяции фиксированы и интерполируется не одна, а несколько функций, то удобнее пользоваться формулой Лагранжа.
| < Предыдущая | Следующая > |
|---|