37. Степень с произвольным действительным показателем

Во множестве R определена степень Ax с действительным показателем.

В выражении Ax число А называют Основанием степени, число X – Показателем степени. Нахождение значения степени называют Возведением в степень.

Степень с действительным показателем

Пусть A Î R, тогда:

1) N Î N;

2)

3)

4) и A ³ 0, если

5) и если то A ³ 0;

6) 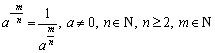и если

7) где определяется следующим образом.

Пусть иррациональное число K записано в виде десятичной дроби, – последовательность его десятичных приближений с недостатком (или с избытком). Для любого действительного числа А > 0 степень с иррациональным показателем определяется равенством

На множестве R не определены отрицательная и нулевая степень числа 0, а также если

Свойства степеней

Допустим, что A, B, C Î R и это такие числа, что все степени имеют смысл. Тогда:

1)

2)

3)

4)

5)

6) если A > 1 и X < Y, то

Если 0 < A < 1 и X < Y, то

7) если 0 < A < B И X >0, то

Если 0 < A < B и X < 0, то

Пример 1. Вычислить

Решение. Используем свойства степеней

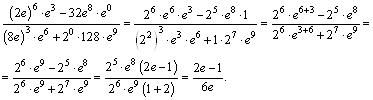
Пришли к ответу:

< Предыдущая		Следующая >