30. Задания
I уровень
1.1. Найдите функцию, обратную данной, если она существует:
1) 
2) 
3) 
4) 
5) 
6) 
1.2. Докажите, что пары функций являются взаимно-обратными:
1)
и 
если 
2)
и 
3)
и 
4)
и 
если 
1.3. Постройте график функции и ей обратной (если она существует) в одной системе координат:
1) если 
2) 
3)
4)
если 
1.4. Найдите точку (точки), принадлежащую кривой для заданного значения Х0:
1) 
2) 
3) 
1.5. Запишите функцию (функции) в явном виде:
1) 
2) 
3) 
4) 
1.6. Найдите соответствующие точки кривой, заданной параметрически, если указаны значения параметра T: 
1) 
2) 
3) 
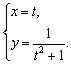
II уровень
2.1. Найдите функцию, обратную данной, и постройте их графики в одной системе координат:
1) 
2) 
3) 
4) 
5) 
6) 
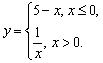
2.2. Определите, обратима ли функция
2.3. Найдите точки пересечения графиков функции 
где 
и обратной ей функции.
2.4. Пусть графиком функции является полуокружность с центром О(0; 0) и радиусом, равным 5, расположенная в нижней координатной полуплоскости. Определите, существует ли функция, обратная данной.
2.5. Пусть задана функция
Найдите промежутки, на которых данная функция обратима.
2.6. Выразите явно У через Х из уравнения и постройте данную линию:
1) 
2) 
если 
3) 
если 
4) 
если 
2.7. Постройте линию, заданную параметрически уравнениями:
1) 
2) 
3) 
4) 
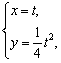
III уровень
3.1. Найдите функцию, обратную данной, и постройте их графики в одной системе координат:
1) 
2) 
3) 
4) 
5) 
6) 
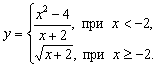
3.2. Докажите, что функция 
обратна сама себе.
3.3. Найдите 
если функция 
обратна функции 
| < Предыдущая | Следующая > |
|---|
