25. Неравенства с модулем
I тип: Неравенство содержит некоторое выражение ![]() под модулем и число вне модуля:
под модулем и число вне модуля:
![]() где
где ![]() (3.27)
(3.27)
Решение зависит от знака числа А.
1. Если ![]() то неравенство (3.27) не имеет решений.
то неравенство (3.27) не имеет решений.
2. Если ![]() то неравенство (3.27) равносильно системе неравенств
то неравенство (3.27) равносильно системе неравенств
![]()
![]() где
где ![]() (3.28)
(3.28)
1. Если ![]() то неравенство (3.28) не имеет решений.
то неравенство (3.28) не имеет решений.
2. Если ![]() то неравенство (3.28) равносильно уравнению
то неравенство (3.28) равносильно уравнению ![]()
3. Если ![]() , то неравенство (3.28) равносильно системе неравенств
, то неравенство (3.28) равносильно системе неравенств
![]()
![]() где
где ![]() (3.29)
(3.29)
1. Если ![]() то решением неравенства (3.29) является множество всех значений Х из ОДЗ выражения
то решением неравенства (3.29) является множество всех значений Х из ОДЗ выражения ![]()
2. Если ![]() то решением неравенства (3.29) является множество всех значений Х из ОДЗ выражения
то решением неравенства (3.29) является множество всех значений Х из ОДЗ выражения ![]() таких, что
таких, что ![]()
3. Если ![]() то неравенство (3.29) равносильно совокупности
то неравенство (3.29) равносильно совокупности
![]()
![]() где
где ![]() (3.30)
(3.30)
1. Если ![]() то решением неравенства (3.30) является множество всех значений Х из ОДЗ выражения
то решением неравенства (3.30) является множество всех значений Х из ОДЗ выражения ![]()
2. Если ![]() то неравенство (3.30) равносильно совокупности
то неравенство (3.30) равносильно совокупности
![]()
II тип: Неравенство, которое содержит выражение с переменной под знаком модуля и вне его:
![]() (3.31)
(3.31)
Где ![]() – некоторые выражения с переменной Х.
– некоторые выражения с переменной Х.
Для решения неравенств типа (3.31) можно использовать следующие способы.
1-й способ: используя определение модуля, получаем равносильную совокупность систем:
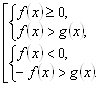
2-й способ: Решаем аналогично решению неравенства (3.29) при дополнительном ограничении на знак выражения ![]()
1. Если
![]() (3.32)
(3.32)
То решением является множество всех значений Х из ОДЗ выражения ![]() которые удовлетворяют условию (3.32).
которые удовлетворяют условию (3.32).
2. Если
![]()
То решением является множество всех значений Х, которые удовлетворяют системе
![]()
3. Если ![]() решение определяется системой
решение определяется системой
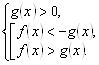
Ответом в решении неравенства (3.31) является объединение всех решений, полученных на этапах 1–3.
3-й способ: метод интервалов.
Для решения необходимо:
1) найти значения Х, для которых ![]()
2) найденные значения Х нанести на числовую ось;
3) определить знак выражения ![]() на всех полученных промежутках;
на всех полученных промежутках;
4) нарисовать кривую знаков;
5) раскрыть модуль, пользуясь рисунком, и получить соответствующее неравенство, которое следует решить вместе с условием принадлежности переменной Х определенному промежутку;
6) в ответе неравенства указать совокупность полученных решений.
III тип: Неравенство содержит несколько модулей и решается двумя способами:
1-й способ: Можно использовать определение модуля и решать совокупность систем неравенств. Этот способ, как правило, не является рациональным.
2-й способ: использовать метод интервалов. Необходимо нарисовать столько числовых осей и кривых знаков, сколько модулей содержится в неравенстве. Для каждого промежутка следует решать полученное после раскрытия модулей неравенство при условии, что переменная Х принадлежит конкретному промежутку. В ответе указывают объединение всех полученных решений.
IV тип: Неравенство вида
![]() где
где ![]() (3.33)
(3.33)
Решается двумя способами:
1-й способ: метод интервалов.
2-й способ: согласно теореме равносильности (см. свойства равносильности неравенств (3.22) и (3.23)) неравенство (3.33) можно возводить в квадрат:
![]()
Решение неравенства (3.33) сводится к решению неравенства
![]()
Аналогично решают неравенства IV типа (3.33), если они заданы со знаками ![]()
V тип: Неравенства, решаемые заменой переменной.
В таком случае выражение с модулем обозначают новой переменной. Неравенство с новой переменной решают до конца (т. е. до возможного получения промежутков решения для новой переменной). Затем возвращаются к старой переменной и решают полученные неравенства с модулем как неравенства I типа.
Пример 1. Решить неравенства:
1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
5) ![]() 6)
6) ![]()
Решение. 1) Решаем как неравенство I типа:
![]()
Получаем ответ: ![]()
2) Решаем как неравенство I типа:
![]()
![]()
Второе неравенство совокупности не имеет решения (соответствующая парабола лежит над осью Ох). Первое неравенство сводится к виду
![]()
Его решение: ![]() это и есть ответ.
это и есть ответ.
3) Решаем как неравенство II типа. Оно имеет решение, если ![]() Поэтому получаем равносильную систему:
Поэтому получаем равносильную систему:
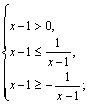
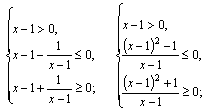
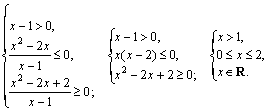
Получаем ответ: ![]()
4) Заданное неравенство может быть записано в виде
![]()
Заменим переменную ![]() Решаем неравенство
Решаем неравенство
![]()
Его решение ![]()
Возвращаемся к переменной Х и решаем совокупность ![]()
Получаем 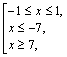
Т. е. приходим к ответу ![]()
5) Для решения неравенства ![]() используем метод интервалов. Запишем неравенство в виде
используем метод интервалов. Запишем неравенство в виде
![]()
Построим числовые прямые и определим знаки выражений, стоящих под модулем (рис. 3.10).
ОДЗ: ![]()
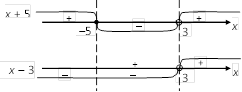 |
Рис. 3.10
А) рассмотрим неравенство на 1-м промежутке. Получаем систему
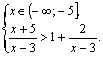 (3.34)
(3.34)
Решаем неравенство
![]()
![]()
![]()
Получаем ![]()
Система (3.34) сводится к системе
![]()
На данном промежутке решений нет.
Б) 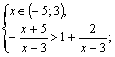
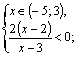
![]()
![]()
![]()
Если ![]() , то
, то ![]() С учетом рассматриваемого промежутка имеем:
С учетом рассматриваемого промежутка имеем:
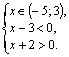
Получаем ![]()
В) 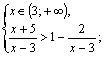
![]()
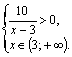
Решением является промежуток: ![]()
Объединим полученные решения и приходим к ответу: ![]()
6) ![]()
ОДЗ: ![]()
Введем новую переменную:
![]() тогда
тогда ![]() и приходим к неравенству вида
и приходим к неравенству вида
![]()
Решаем его
![]()
![]()
Используем метод интервалов (рис. 3.11).
Рис. 3.11
![]() Запишем полученное решение в виде совокупности:
Запишем полученное решение в виде совокупности: ![]()
Вернемся к переменной Х:

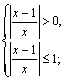 (3.35)
(3.35)
![]() – выполняется при любых
– выполняется при любых ![]()
С учетом ОДЗ второе неравенство системы (3.35) равносильно системе
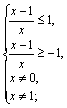
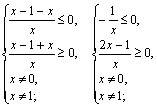
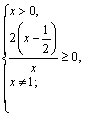
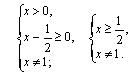
Получаем ответ: ![]()
| < Предыдущая | Следующая > |
|---|