17. Дробно-рациональные уравнения

Стандартный вид дробно-рационального уравнения:

(3.8)

Где – многочлены.

Область допустимых значений (ОДЗ) данного уравнения: Решение уравнений (3.8) сводится к решению системы

Дробно-рациональные уравнения вида

Где – многочлены, можно решать, используя основное свойство пропорции:

К основному методу решения дробно-рациональных уравнений относится также метод замены переменной.

Некоторые специальные приемы будут рассмотрены далее на примерах.

Пример 1. Решить уравнение

Решение. Сводим заданное уравнение к стандартному виду (3.8):

т. е.

Его решением будет решение системы

т. е.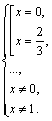

Значит, решением заданного уравнения является

Пример 2. Решить уравнение

Решение. Применим основное свойство пропорции с учетом ОДЗ уравнения:

Получаем:

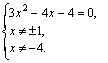
Откуда

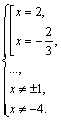
Оба корня являются решениями, так как подходят по ОДЗ. В ответе имеем:

Пример 3. Решить уравнение

Решение. Группируем слагаемые

Заменяем

откуда

т. е. и

Получаем уравнение или, то же самое,

Полученное уравнение имеет корни:

Возвращаемся к переменной Х:

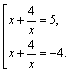
В результате приходим к совокупности 2-х квадратных уравнений

Которые решаем на ОДЗ: Приходим к ответу

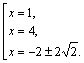
Пример 4. Решить уравнение

Решение. Выделим в левой части уравнения полный квадрат суммы:

Получаем уравнение, которое приобретает вид

Заменяем и приходим к уравнению

Решая его, найдем корни:

Возвращаемся к старой переменной:

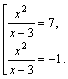
Решаем полученные уравнения по свойству пропорции (с учетом ОДЗ):

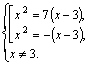
Приходим к ответу

Пример 5. Решить уравнение

Решение. Введем замену:

Тогда и получим уравнение

Решаем его:

т. е.

Решая квадратное уравнение, находим корни:

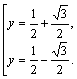
Вернемся к переменной Х:

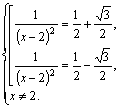
Решаем первое уравнение:

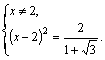
Второе уравнение не имеет решения, так как

Получили ответ:

< Предыдущая		Следующая >