92. Однородная система линейных уравнений (ОСЛУ)
Пусть дана однородная система M Линейных уравнений с N неизвестными:
 (2)
(2)
Каждое решение системы (2) вектор в арифметическом N-мерном пространстве Рn. Очевидно, что нулевой вектор 0 = (0, 0, ...,0) является решением системы (1). Обозначим через Х0 множество решений системы (1). Тогда имеет место следующая теорема о структуре множества решений однородной системы линейных уравнений.
Определение 1. Подмножество L ≠ Æ векторного пространства V называется подпространством V, если
1) (" A, B € L) A + B € L; 2) (" A € L) (" a € R) aA € L.
.Теорема 2. Множество Х0 Всех решений ОСЛУ (2) образует подпространство размерности n - r арифметического n-мерного пространстве Рn, Где N - число неизвестных в системе, r - ранг матрицы системы.
Доказательство. В силу сказанного выше Х0 Í Рn , Х0 ≠ Æ . Пусть вектора A = (A1,A2, ..., AN), B = (B1,B2, ..., BN) € Х0. Тогда по определению выполняются следующие системы верные равенства:
Ai1A1 + Ai2A2 + ... + AinAN = 0, I = 1, 2, ...,M; (7)
Ai1B1 + Ai2B2 + ... + AinBN = 0, I = 1, 2, ...,M. (8)
К каждому равенству системы (7) прибавим почленно соответствующее равенство системы (8) и получим систему верных числовых равенств:
Ai1(A1 + B1) + Ai2(A2 + B2) + ... + Ain(AN + BN) = 0, I = 1, 2, ...,M,
Из которой по определению следует, что вектор A + B = (A1 + B1,A2 + B2, ..., AN + BN) решение системы (6) , т. е. A + B € Х0.
Умножая обе части равенств (8) на произвольное число g € Р получаем систему верных числовых равенств:
Ai1(GA1) + Ai2(GA2) + ... + Ain(GAN) = 0, I = 1, 2, ...,M.
Отсюда следует, что для любого вектора A € Х0 и любого числа G € Р вектор GA € Х0 . Таким образом по определению Х0 подпространство векторного пространства Рn .
Пусть R =rangA . Докажем, что dimХ0 = N - r. Для этого решая систему (6) методом Гаусса приведем ее с помощью элементарных преобразований и преобразований вычеркивания нулевых уравнений к ступенчатому виду. При этом матрица системы с помощью элементарных преобразований строк и преобразований вычеркивания нулевых строк перейдет к матрице ступенчатого вида, которая будет содержать R строк. При этом в полученной системе ступенчатого вида будет R уравнений. Будем предполагать, что главными неизвестными в полученной системе ступенчатого вида будут первые R неизвестных X1, X2, ..., xr и полученная система имеет вид:
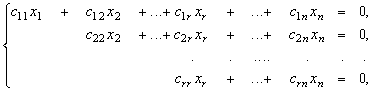 (9)
(9)
Где все коэффициенты С11 , С22 , ..., сrr не равны нулю, неизвестные X1, X2, ..., Xr - главные, а неизвестные Xr+1, ..., Xn - свободные. Пусть Xr+1 = AR+1 , ..., Xn = AN , где AI € P , I = R+1, ...,N. Из уравнений системы (9) выразим значения главных неизвестных через свободные и получим:
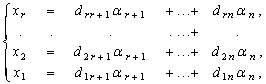
Где Dij € P; I = 1, 2, ..., R; J = R + 1, ..., N. Запишем общее решение системы (6) в виде вектор-столбца:
XT = 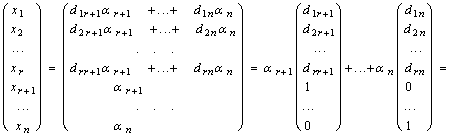
=AR+1X1T + ...+ ANXN-RT.
Таким образом каждое решение системы (6) линейная комбинация N-r решений:
X1 = (D1R+1, D2R+1, ..., Drr+1, 1, ..., 0), ..., XN-r = (D1N, D2N, ..., Drn, 0, ..., 1). (10)
Рассмотрим матрицу, составленную из координат этих векторов,
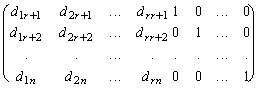 .
.
Так как ранг этой матрицы равен N-r , то строки ее линейно независимы и система векторов (10) линейно независима и по определению базиса она образует базис подпространства Х0 решений однородной системы (6). Следовательно, dim Х0 = N-r . Теорема доказана.
Определение 1. Фундаментальной системой решений однородной системы называется базис подпространства решений системы.
Следствие 1. Любая однородная система линейных уравнений обладает фундаментальной системой решений, состоящей из n-r решений.
Если X1, X1, ..., XN-r - фундаментальная система решений однородной системы (6), то она обладает свойствами:
1) она линейно независима,
2) любое решение X системы (6) единственным образом представляется в виде X = AR+1X1 + AR+2X2 + ...+ ANXN-R; AI € P, I = R+1, ...,N.
Далее множество решений Х0 однородной системы есть линейная оболочка натянутая на фундаментальную систему решений:
Х0 =L(X1, X1, ..., XN-r).
Фундаментальную систему решений однородной системы можно найти по методу, изложенному в доказательстве теоремы 2.
Пример 1. Найти фундаментальную систему решений системы![]()
![]()
Приведем систему элементарными преобразованиями к ступенчатому виду:
![]()
Пусть X3 = A , X4 = B. Тогда Х2 = -2A - 3B , Х1 = -A - 2B . Отсюда общее решение системы
ХТ =  ,
,
И фундаментальная система решений: Х1 = (-1, -2, 1, 0), Х2 = (-2, -3, 0, 1).
По доказанной теореме однородная система имеет только нулевое решение тогда и только тогда, когда размерность подпространства ее решений равна 0, т. е. при N-r = 0, N =r , определитель системы не равен нулю. Тогда получаем следствия.
Следствие 2. Однородная система n линейных уравнений c n неизвестными имеет только одно нулевое решение тогда и только тогда когда определитель системы не равен нулю.
Следствие 3. Однородная система n линейных уравнений c n неизвестными имеет ненулевое решение тогда и только тогда когда определитель системы равен нулю.
| < Предыдущая | Следующая > |
|---|