61. Угол между прямыми. Условие перпендикулярности двух прямых на плоскости

Определение 1. Углом между пересекающимися прямыми Называется величина любого из углов, который образуется при пересечении прямых. Если прямые параллельны или совпадают, то угол считается равным нулю.

Пусть A и B две прямые, заданные своими общими уравнениями в прямоугольной системе координат:

A: A1X + B1Y + C1 = 0,

B: A2X + B2Y + C2 = 0,

A12 + B12 ≠ 0, A22 + B22 ≠ 0.

Рассмотрим нормальные векторы N1 = (A1,B1), N2 = (A2,B2) прямых A и B. В силу теоремы об углах с соответственно перпендикулярными сторонами угол j между прямыми A и B равен углу между нормальными векторами N1 и N2. По определению скалярного произведения векторов

N1N2 = |N1|×| N2|cos J.

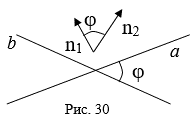
Отсюда находим формулу косинуса угла между прямыми A и B:

. (7)

По формулам синуса и тангенса угла между векторами на плоскости находим:

, (8)

. (9)

Отметим, что формула (9) наиболее удобна, так как не содержит радикалов, но не верна в том случае, когда прямые A и B перпендикулярны.

Заметим, что прямые A и B перпендикулярны тогда и только тогда, когда нормальные векторы N1 и N2 этих прямых ортогональны. По условию ортогональности векторов последнее равносильно тому, что скалярное произведение N1N2 = 0. Так как N1N2 = A1A2+B1B2, то получаем теорему.

Теорема 2. Прямые A И B Перпендикулярны тогда и только тогда, когда

1N2 = A1A2+B1B2 = 0. (10)

Если прямые заданны уравнениями

Y = K1X + B1, Y = K2X + B2

с угловым коэффициентом, то из формулы (9) находим формулу для нахождения угла между прямыми, заданными уравнениями с угловыми коэффициентами:

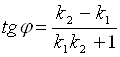. (11)

Условие (10) перпендикулярности прямых в этом случае принимает вид:

K1K2 + 1 = 0. (12)

< Предыдущая		Следующая >