112. Приведение квадратичной формы к каноническому виду. Метод Лагранжа. Закон инерции
Теорема 1. Любую квадратичную форму
F(X1, x2,…, Xn) = F(X)= ![]() . (1)
. (1)
невырожденным линейным преобразованием X=TY, где X = (X1, X2,…, Xn)T, Y = (Y1, Y2,…, Yn)T, можно привести к виду
H(Y1, Y2,…, Yn) = ![]() . (2)
. (2)
Представление квадратичной формы в виде (2) называется Каноническим видом квадратичной формы. Коэффициенты называются Каноническими коэффициентами. Матрица квадратичной формы канонического вида - диагональная матрица.
Доказательство. Докажем теорему методом математической индукции по числу N переменных в квадратичной форме F. Пусть N =1. Тогда квадратичная форма F имеет вид F = B11X12 и является квадратичной формой канонического вида.
Предположим что теорема доказана для всех квадратичных форм, имеющих меньше чем N переменных, и докажем ее для квадратичной формы F, имеющей N переменных. Рассмотрим два случая.
1. Среди диагональных коэффициентов B11, B22, …, Bnn есть отличный от нуля. Пусть, например, B11 ≠ 0. Рассмотрим квадратичную форму ![]() , которая содержит такие же члены с неизвестным, как и наша форма F. Тогда разность
, которая содержит такие же члены с неизвестным, как и наша форма F. Тогда разность
F(X1, X2,…, Xn) -![]()
![]()
Будет квадратичной формой, содержащей только неизвестные X2,…, Xn. Отсюда
![]() .
.
Вводим неизвестные
![]() , (3)
, (3)
И получим
![]() , (4)
, (4)
Где G( Y2,…, Yn) - квадратичная форма от не более чем N -1 неизвестной. Преобразование (3) невырожденное, так как матрица этого преобразования равна
 ,
,
И определитель равен B11 ≠ 0. Обратное ему преобразование тоже невырожденное и приводит форму F в форму (4). По индуктивному предположению квадратичную форму G( Y2,…, Yn) невырожденным преобразованием переменных Y2,…, Yn можно привести к квадратичной форме канонического вида. Это преобразование можно рассматривать как невырожденное, при котором неизвестная Y1 остается без изменения. Оно приводит квадратичную форму (4) к каноническому виду. Таким образом, невырожденным преобразованием переменных форма F приводится к каноническому виду.
2. Все диагональные коэффициенты B11, B22, …, Bnn равны нулю. Тогда среди коэффициентов формы должен быть отличный от нуля. Так как в противном случае форма тождественно равна нулю и являлась бы канонической. Пусть, например, B12 ≠ 0. Сделаем вспомогательное преобразование переменных так, чтобы в квадратичной форме появился квадрат. Сделаем преобразование переменных:
X1 = Z1 + Z2, X1 = Z1 - Z2, X3 = Z3,…, Xn = Zn.
Оно невырожденное, так как матрица этого преобразования равна
 ,
,
И определитель ее равен 2 и не равен нулю. В результате этого преобразования член нашей формы примет вид
2 a12X1X2 = 2 a12( Z1 + z2)(Z1 - z2) = 2 a12Z12 - 2 a12 z22,
И форме появляется ненулевой коэффициенты у квадратов двух переменных. Эти члены не могут сократиться с остальными членами, так как во все остальные члены войдет хотя бы одна из переменных Z3,…, Zn. Полученную квадратичную форму по первой части доказательства можно привести к квадратичной форме канонического вида невырожденным преобразованием переменных.
Пример. Методом Лагранжа привести квадратичную форму к каноническому виду
![]() ,
,
И найти преобразование переменных, приводящую эту форму к каноническому виду.
Решение. Так как в форме нет квадратов переменных, то сделаем преобразование переменных
X1 = Z1 + Z2, X1 = Z1 - Z2, X3 = Z3
Матрица этого преобразования равно
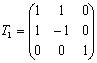
И квадратичная форма преобразуется к виду
![]() .
.
Выделим полный квадрат из членов, содержащих X1
![]()
![]() .
.
Полагаем Y1 =Z1 +(5/2)Z3, Y2 = Z2+(1/2) Z3, Y3 = Z3 приведем квадратичную форму к каноническому виду
![]() .
.
Выразим неизвестные Z1 =Y1 - (5/2)Y3, Z2 = Y2-(1/2) Y3, Z3 = Y3. Последнее преобразование имеет матрицу
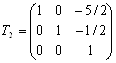 .
.
Тогда преобразование, переводящее данную квадратичную форму к форме канонического вида имеет матрицу, равную произведению матриц.
 ,
,
Преобразование переменных имеет вид:
X1 =Y1 + Y2 - 6Y3, X2 =Y1 - Y2 - 4Y3, X3 = Y3.
| < Предыдущая | Следующая > |
|---|